I hear that rms is the ac value which would produce the same heat effect as a dc value... but I don't understand why this rms is different from average value. I also read that the average value of an ac value is zero for a full circle. But why is the rms value of an ac half circle not the same value of that ac half circle .
Asked
Active
Viewed 2,305 times
0
-
4This is pretty much a duplicate of AC Effect Value. See my answer to show a worked example. – Transistor Nov 12 '18 at 18:52
-
There's more than one kind of average RMS (also known as "quadratic mean") is one of them. – Solomon Slow Nov 12 '18 at 19:14
-
RMS is Root Mean Square, so the first step is squaring all the values, both positive and negative, which results in all the values now positive, while that does not happen with an average... – Solar Mike Nov 12 '18 at 19:22
-
Well, for one thing the average (mean) of mains AC is 0V, but RMS is e.g. 230V. Very little heating at 0V DC ;) – marcelm Nov 12 '18 at 20:39
2 Answers
1
The average value is the mathematical average of the signal. If you have a 1V amplitude sine wave, it periodically oscillates between -1V and +1V, so the average of that sine wave is 0V.
But obviously, you aren't delivering an average of 0W. In reality, you don't have negative voltages. A resistive load (and any load for that matter) simply sees a voltage being applied to it, regardless of its direction. So, how do we mathematically get the actual "average" of the power being applied?
Square the signal (to make it all positive), take the average of the squared values (mean-square value) then "undo" it (square root it). That's your actual "average" voltage being applied, hence the term Root-Mean-Square.
Well, it turns out that, for a sinusoid, the RMS voltage equates to $$V_{RMS}=\sqrt\frac{V_{max}^2}{2}=\frac{V_{max}}{\sqrt2}$$
Sean M
- 136
- 8
0
I hear that rms is the ac value which would produce the same heat effect as a dc value
You got that back to front - the RMS value is the DC value that produces the same heat.
Power is related to voltage squared. In other words if 1 volt produces 1 watt in a 1 ohm resistor, 2 volts produces 4 watts in the same resistor so, to calculate the heating effect of a voltage waveform you must square all the instantaneous values of that waveform then calculate the average, then take the square root to get RMS.
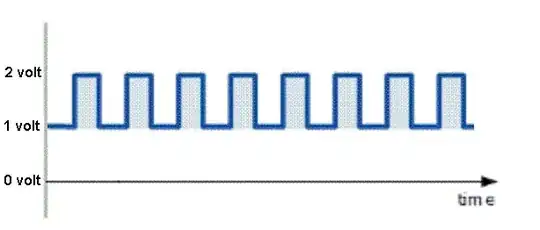
Consider a simple example of the waveform that is 1 volts for 1 milli second then 2 volts for the next millisecond repeating: -
The power in the first 1 millisecond is 1 watt and the power in the second millisecond is 4 watts because of \$V^2/R\$.
The average power is \$\dfrac{1+4}{2}\$ watts = 2.5 watts.
If you calculated the equivalent voltage that dissipates 2.5 watts in a 1 ohm resistor, it would be \$\sqrt{2.5}\$ volts = 1.581 volts whereas the average of the two voltages is only 1.5 volts.
Andy aka
- 456,226
- 28
- 367
- 807