2

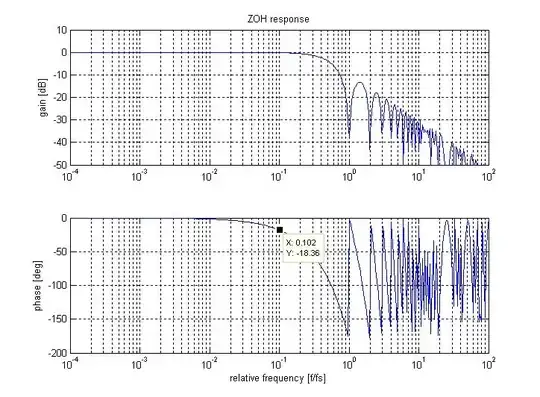
I heard a rule of thumb this morning indicating that modeling a discreet system as continuous using a second order padé approximation for the zero order hold will result in a 2Db loss of gain margin, and a 7° loss of phase margin, provided the sample rate is sufficiently faster than the bandwidth of the system. I have found no mention of this in my textbooks.

Has anyone else heard of this rule of thumb?

If so, is there a reasonable set of limitations for it's application?

Tom Davies
  • 316
  • 1
  • 2
  • 11
2NinerRomeo
  • 131
  • 1
  • 5
  • "provided the sample rate is sufficiently faster than the bandwidth of the system" sounds like it needs some qualification before anything else could be done. Is "just" 2x enough? 5x? 10x? – Martin Thompson Jul 28 '11 at 10:34
  • I'd say that's part of my question. I have no idea what a sufficient sample rate would be. I use a rule of thumb that an estimator should have 6x the bandwidth of a controller, but it may be quite a leap to go from there to my current problem. Perhaps a factor of two is good enough. – 2NinerRomeo Jul 28 '11 at 18:23

1 Answers1

2

One rule of thumb is that if the sample rate is > 10x the highest frequency of interest then a continuous analysis is a reasonable approximation. However you can check this more accurately.

The frequency response of a ZOH can be estimated from the Laplace transform of its impulse response: Lzoh{s} = (1-e^-sT)/s, and you can substitute s=jw=j*2*pi*f to calculate the frequency response. With a sampler in front, with no aliasing (band limited input) the net result is L{s}=(1-e^-sT)/(sT).

You can simulate this in Matlab or Octave. The result is that at one tenth the sample rate (f=fs/10), the gain is down only 0.15dB, but the phase is shifted -18 degrees. That is quite a bit of phase distortion. These effects need to be taken into account in any signal processing chain, so the end result is what you intended.

zoh response

mixed_signal_old
  • 251
  • 1
  • 4