If 75% of radioactive material remains, how many half-lives have elapsed?

Question

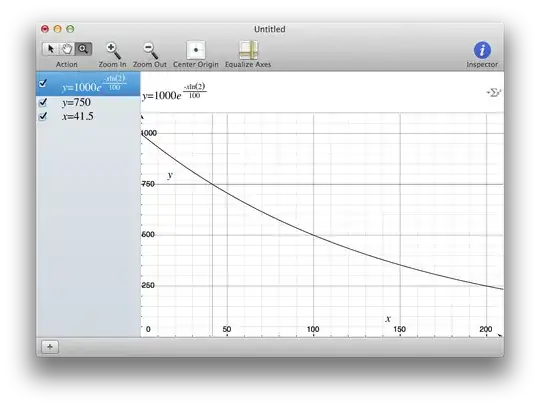
Radioactive element A radioactively decays into material B. If 75% of A and 25% of B are present, how many half-lives of material A have elapsed?

I was recently taught that the correct answer is "one half of a half-life has elapsed". However, due to the fact that the amount of radioactive material remaining scales exponentially (logarithmically) instead of in a linear fashion, wouldn't the answer be less than one half of a half-life?

Answer 1

@gerrit provided a formula, but without stating the reasoning behind it.

Radioactive decay is an exponential function. After $n$ half-lives, the amount of the original material remaining is

$$\textrm{amount remaining after}\ n\ \textrm{half-lives} = \left(\frac{1}{2}\right)^n$$

Therefore, you want to solve

$$\begin{align*} \left(\frac{1}{2}\right)^n &= \frac{3}{4}\\ \log_\frac{1}{2} \left(\frac{1}{2}\right)^n &= \log_\frac{1}{2} \frac{3}{4}\\ n &= \frac{\log \frac{3}{4}}{\log \frac{1}{2}} = \frac{\log \frac{3}{4}}{- \log 2} \approx 0.415 \end{align*}$$

Answer 2

The other answers are entirely correct. But I like graphical representations.

From http://en.wikipedia.org/wiki/Radioactive_decay we see the decay formula is:

$$N(t) = N_0e^\frac{-t}{τ}$$

Where N₀ is the starting number of nuclides and τ is the mean lifetime. We also see that the half-life is

$$t_{1/2} = τ ln(2)$$

Substituting for τ, we get:

$$N(t) = N_0e^\frac{-tln(2)}{t_{1/2}}$$

So for example if we have N₀ = 1000 and t_1/2 = 100 we can plot the following graph:

_{Note that the horizontal axis is the t-axis.}

We see the following:

• At t=100 (one half life), N(t) is 500, half of 1000, as expected
• At t=200 (two half lives), N(t) is 250, 1/4 of 1000, as expected
• We intersect the curve with a line at N(t) = 750. Here we can see this occurs at about t=41.5 as predicted by the other answers.

Answer 3

You can use simple logarithms to calculate the answer. The number of half-lives that have elapsed can be calculated with

$$ - \frac{\log{f}}{\log{2}} $$

where $f$ is the fraction that remains.

So plugging in the numbers gives

$$ - \frac{\log(0.75)}{\log(2)} = 0.415 = 41.5\% $$