Can someone please provides me with the recursion relations of Associated Legendre Polynomials when using Schmidt quasi-normalization? I need that in the context of Geomagnetism to obtain the Spherical Harmonics coefficients g and h.
Asked
Active
Viewed 613 times
2
-
The answers here might help with this also, for future browsers: https://earthscience.stackexchange.com/q/22368/14123 – WJB Jun 15 '21 at 09:14
1 Answers
2
FYI, the usual reference relied on for the equations used in geomagnetism is:
- Langel, R. A. "Chapter four: Main field." Geomagnetism, edited by JA Jacobs (1987).
If it wasn't for lockdown I'd have copied from the book locked in my office to make sure I got it right...but until someone corrects me...
The Schmidt quasi/semi-normalisations for the associated Legendre polynomials are given by these recursions, in the form you'd actually use for calculations typically:
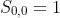
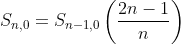
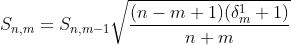
Note that if you use Schmidt normalisation of Legendre polynomials from a given software language to do calculations, you do not want to include the Condon-Shortley phase factor of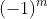 
. So check if it is included in the Legendre polynomial and/or normalisation formula.
Edit: Some links to open source geomagnetism compatible software for calculating Schmidt normalised associated Legendre polynomials.
Python: ChaosMagPy
Python/Fortran-95: SHTools
WJB
- 921
- 6
- 10
-
That exactly what I was looking for, except I couldn't find the mentioned reference anywhere on the web, so thanks for the hint. However, I really need a confirmation about the formula correctness including the derivatives too. – Ayoub Aug 24 '20 at 16:06
-
I don't think there is a digital version of Langel (1987) anywhere online, but I just found I could view enough of the following reference through Google Books to confirm the equations: Wertz, J. R. "Spacecraft Attitude Determination and Control", (1978). Use the "Search inside" option and search for "Appendix H", you can see the first few pages about Schmidt normalisation. – WJB Aug 24 '20 at 16:27
-
That was useful, thanks again! So, the factors S are used with Gauss functions to obtain Schmidt functions, where: P_Schmidt = S * P_Gauss. But, it's still a long way to go with. I would love to compute directly the P_Schmidt functions since we know that there's recursion relations for them out there. – Ayoub Aug 24 '20 at 17:33
-
Are you actually after the final recursive formula for the Schmidt P_n^m(cos(theta)) functions themselves, or are you ultimately trying to write code to calculate these values for geomag problems? I can add links to open source code in a few languages much more easily than I can work back and type up the formula working from those codes right now! – WJB Aug 24 '20 at 19:15
-
Exactly I'm trying to implement a code to calculate those values, any open source code is welcomed! but I can't just take the code without the formula since I need to document that. – Ayoub Aug 24 '20 at 21:22
-
I understand, I've added links to the two clearest and most accessible examples of code. There also a C library, Fortran-77, Python/C, and Matlab code I can dig out if those would be better. – WJB Aug 24 '20 at 22:49
-
To work out the final recursion formula, you need to take the normalisation formula above, combine them with the unnormalised Legendre recursion formula, and cancel them down. There's a special case for the first couple of terms, and for geomag use, the d.P_n^m(cos(theta))/d.theta terms needed are actually equivalent to values of P_m^{n+1}(cos(theta)). – WJB Aug 24 '20 at 22:57
-
@WJB you might be able to shed some light on this; I've asked How can I verify my reconstructed gravity field of Ceres from spherical harmonics? and there might be some helpful information at How are the coefficients in the EGM96 model normalized? but I can't tell. I want to generate the gravitational potential for Ceres so I can propagate orbits around it (e.g. Dawn spacecraft) but I don't know how to get it from those coefficients. I want to do it myself rather than use a library. – uhoh Sep 16 '20 at 02:25