Frequency spectrum of interpolated sine

Question

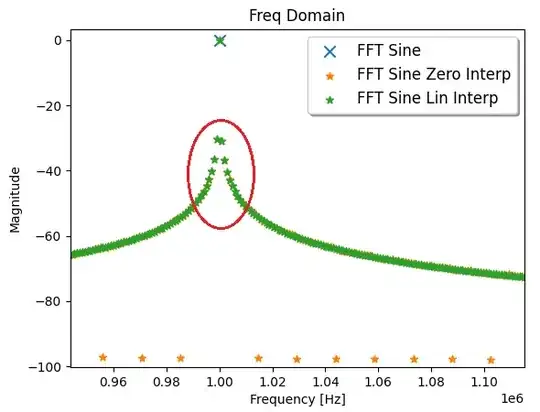
When interpolating a sine wave in Python, it seems I get a lot of additional frequencies closely around the fundamental. Why is that the case? I would have expected a more or less similar spectrum, with images of the original spectrum at higher frequencies. How can I get a "clean" interpolated signal? I tried zero-order hold and linear interpolation, however that didn't seem to affect those frequencies around the fundamental.

import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.fftpack import fft
from scipy import interpolate
M = 32 # Oversampling
M_interp = 16
f_in = 1e6
amp_in = 1
f_s = f_in * M
f_s_interp = f_s * M_interp
N = int((f_s/f_in) * 1024) # Nr of samples
N_interp = N * M_interp
ax_t = np.linspace(0, float((1 / f_s) * (N - 1)), num=int(N), dtype=float)
ax_t_interp = np.linspace(0, float((1 / f_s) * (N - 1)), num=int(N_interp), dtype=float)
ax_f = np.fft.fftfreq(N, 1 / f_s)[0:N // 2]
ax_f_interp = np.fft.fftfreq(N_interp, 1 / f_s_interp)[0:N_interp // 2]
x = amp_in * np.cos(2 * math.pi * f_in * ax_t)
f_int_zero = interpolate.interp1d(ax_t, x, kind='zero')
f_int_lin = interpolate.interp1d(ax_t, x, kind='linear')
y_int_zero = f_int_zero(ax_t_interp)
y_int_lin = f_int_lin(ax_t_interp)
plt.step(ax_t, x, where='post', linewidth=2, label ='Sine')
plt.step(ax_t_interp, y_int_zero, linewidth=2, label ='Sine Interp Zero')
plt.step(ax_t_interp, y_int_lin, linewidth=2, label ='Sine Interp Lin')
plt.xlim(0, 1.25e-6)
plt.legend(loc='upper right', shadow=True, fontsize=12)
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.title('Time Domain')
plt.figure()
plt.scatter(ax_f, 20np.log10(np.divide(np.abs(fft(x)), N/2))[0:N // 2], label = 'FFT Sine', marker='x', s = 80)
plt.scatter(ax_f_interp, 20  np.log10(np.divide(np.abs(fft(y_int_zero)), N_interp / 2))[0:N_interp // 2], label ='FFT Sine Zero Interp', marker='')
plt.scatter(ax_f_interp, 20  np.log10(np.divide(np.abs(fft(y_int_lin)), N_interp / 2))[0:N_interp // 2], label ='FFT Sine Lin Interp', marker='*')
plt.ylim(-100, 5)
plt.xlim(0, 2.5e6)
plt.legend(loc='upper right', shadow=True, fontsize=12)
plt.xlabel('Frequency [Hz]')
plt.ylabel('Magnitude')
plt.title('Freq Domain')
plt.show()

UPDATE: I coded the zero-order hold myself as shown below, which eliminated the frequencies closely around the fundamental.

y_int_zero = np.zeros(len(ax_t_interp))
for i in range(len(ax_t_interp)):
    sample_index = int(i / M_interp)
    y_int_zero[i] = x[sample_index]

Well linear interpolation, done correctly, should perform a hella lot better than zero-order hold. You either need more points in your table or higher order interpolation. — robert bristow-johnson, Oct 18 '23 at 19:40
Or you might consider coding a half of the sine with 5th or 7th order odd-symmetry polynomial. — robert bristow-johnson, Oct 18 '23 at 19:42
And BTW, the points depicted in you spectrum of ZOH don't look correct at all. — robert bristow-johnson, Oct 18 '23 at 19:46
The "correct" way of interpolating is sinc interpolation. See https://en.wikipedia.org/wiki/Whittaker%E2%80%93Shannon_interpolation_formula#:~:text=The%20Whittaker%E2%80%93Shannon%20interpolation%20formula,to%20the%20works%20of%20E. — Hilmar, Oct 18 '23 at 21:06
Thanks @robertbristow-johnson due to your comment I tried to just hand-code the zero-order hold myself, result looks much better — MisterFilter, Oct 19 '23 at 08:11

score 0 · Answer 1 · answered Oct 19 '23 at 16:04

It looks like the OP's code is set up such that the number of samples is dependent on the input sample rate.

N = int((f_s/f_in) * 1024) # Nr of samples

The extra frequencies that are shown are due to spectral leakage, not the interpolation approach. If the sampling rate is an integer number of cycles, there won't be any spectral leakage- but this isn't representative of how one would often use the FFT to analyze a waveform (as the frequency often isn't conveniently a single tone or known beforehand). If the interpolation used causes this integer ratio rule to be broken, the spectral leakage will be visible.

To address spectral leakage concerns, window the waveform prior to computing the FFT. To interpolate with minimum distortion, zero insert to the new rate (insert $I-1$ zeros in between each sample). This will replicate the spectrum, and the replication in each Nyquist Zone (DC to the original sampling rate), will be exact with no distortion other than possible scaling. Then pass this waveform through an interpolation filter, which ideally passes the primary spectrum of interest with no distortion and completely rejects all the images. Doing this perfectly is not feasible, but at the expense of filter delay and complexity we can minimize the distortion to any level desired.

Least squares multiband filter design (using scipy.firls in Python) is ideal for this application as we can concentrate the nulls at all the image locations. This is demonstrated in the following graphic showing the replicated spectrum after a inserting 3 zeros between each sample (upsample by 4), along with the response of the multiband interpolation filter designed with firls:

The filter was implemented as a 29-tap FIR filter. The plot below shows how the filter compares to a Sinc interpolator (very bad due to truncation), and an improved windowed Sinc both as 32 taps. Even with 3 less taps, we can see that the multiband filter still has slightly better performance than the windowed Sinc over most of the image regions and is just as easy to generate, so would be my recommended approach to interpolation.

Frequency spectrum of interpolated sine

1 Answers1