Consider some signal in frequency domain:

the maximum length of which corresponds to the half of the original signal ($N/2$), here $N=32$. It is known that the bandwidth of each sample is $2/N$, so in this case I'll have the bandwidth of $1/16=0.0625$ for all samples except first and the last for which the bandwidth is $1/32 = 0.03125$.
I'm a bit confused about such definition of bandwidth, because if I plot it (for example for the second sample):
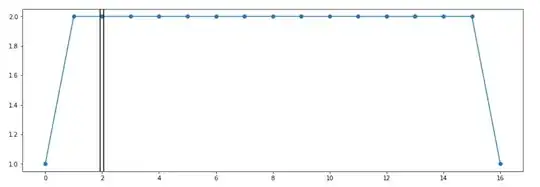
I get some strange visualization. For me it is clear that the total bandwidth should be equal to the sum of all the badwidths for all the samples.
What's wrong in my interpretation of bandwidth on the second plot or maybe I found incorrect definition of bandwidth?


Pythonfunctionnp.fft.fft()even for the first and last bins, that's why it caused even more confusion... – Curious May 07 '22 at 14:21np.fft.fft()corresponding to the time-domain amplitudes, I found that if I divide the result of this function by $N/2$ (or multiply by $2/N$) and also divide the first and last samples by $N$ (as in the book!), I'll get the desired result - amplitudes in frequency domain will unambiguously correspond to amplitudes in time-domain, but why I should divide by $N/2$ - this is the main question for me – Curious May 07 '22 at 14:49