What is Frequency Resolution?

Question

Im trying to tackle the following problem while still not having a firm idea on what "frequency resolution" means :

Suppose we sample a continuous time signal with sampling period Ts = 1/2000, and then use a window of length 1000 on the resulting discrete time signal. If we transform it using a 2000 point DFT what would its frequency resolution be ?

Can anyone help me figure this out ?

Do you want potential plot resolution with interpolation, peak location estimation resolution given an S/N, result bin separation, or peak separation resolution with a separation criteria? All these produce different frequency resolutions for the same length DFT. — hotpaw2, Feb 01 '19 at 21:33
@hotpaw2 I would be interested if you can talk about these resolutions in this or a different informative question. — Dsp guy sam, Apr 16 '20 at 22:05

Tom Huntington · Answer 1 · 2022-04-18T02:23:26.183

5

Edit:

I've come to realize that my definition below of "Frequency Resolution" is completely wrong (as well as OP's question). Frequency resolution should be defined in terms of how closely the window function (in frequency space) approximates the Dirac delta function. This is because a product of the window and the signal in the time domain becomes a convolution in the frequency domain (and a convolution with the Dirac delta function is just a sampling i.e. a perfect frequency resolution) The fatter the mainlobe and the higher the sidelobes, the worse the frequency resolution. Additionally, Time resolution can be quantified as the variance of the window function in the time domain.

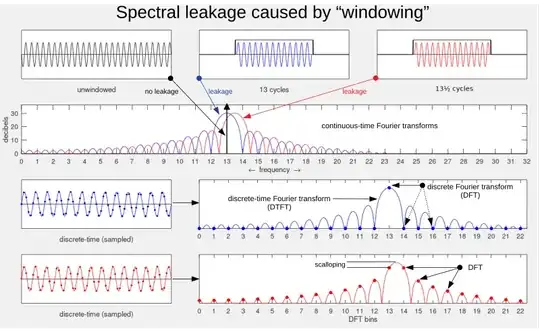
Frequency Resolution is not Bin Resolution/Width. In the graph below notice that the lobes dont get closer (frequency resolution) even though bin width is decreasing.

Credit: Dan Boschen

Frequency resolution is rather a property of the Fourier transform of the rectangular function (i.e. the sinc function).

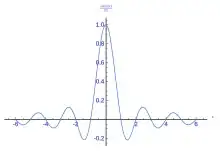
We must window functions to work with Fourier transforms (even when working theoretically). As a consequence we are always working with $f(t)w(t)$ rather than the function $f(t)$ itself (here $w(t)$ is a rectangular function). By the Convolution theorem the Fourier transform of a windowed function is always a convolution of $\hat{f}$ with $\hat{w}=$ sinc. Notably when $f$ is sinusoidal, $\hat{f}$ will be a Dirac delta function and the convolution will just be a sampling of a sinc function. Thus we periodically lose frequencies completely when windowing, the periodicity of this loss is the frequency resolution.

Since, on windowed functions, the DTFT is a periodic approximation of the CTFT it also acquires these properties.

The confusion arises because when we dont pad zeros to the DFT (i.e. only sample $f(t)w(t)$ where $w(t)=1$), the bin width is equal to the Frequency resolution.

However, we may also pad zeros (i.e. also sample $f(t)w(t)$ where $w(t)=0$) and this results in the DTF better interpolating the DTFT of $f(t)w(t)$. Confer with the first graph.

To see why the Fourier transform of the rectangular function is the a sinc funcion watch this video and consider the winding of the sinusoidal functions (its quite involved though)

To answer OP's example the bin resolution is $$\frac{F_s}{N} = \frac{2000}{2000}=1$$ where $F_s=2000$Hz is the sampling rate, and $N$ the DFT size.

The frequency resolution is what the bin resolution would be if we just sampled in the window (no zero padding)

$$\frac{F_s}{M} = \frac{1}{T}=2$$ where $M$ is the number of samples in the window, $T$ is the duration of the sample, and $F_s=M / T$.

edited Apr 18 '22 at 02:23

answered Apr 16 '20 at 00:34

Tom Huntington

376
3
18

2

Nice answer Tom. Also to add if not clear we often don't actually use a rectangular window, but other windows that taper which serve to significantly decrease the sidelobes (improve dynamic range) at the expense of degrading frequency resolution further. One of my favorite classic papers on this and the applications of the DFT in general is by fred harris. I think you'll really enjoy it if you haven't already seen it: http://web.mit.edu/xiphmont/Public/windows.pdf – Dan Boschen Apr 16 '20 at 02:23
But all that said, you never really answered his more detailed question--- that would make your answer even better! – Dan Boschen Apr 16 '20 at 02:25
Disagree with this terminology. The interpolated sinusoidal frequency peak position in zero noise can have a much higher resolution and accuracy than the bin spacing of either the zero-padded or non-zero-padded DFT. Both really depend on the min S/N ratio, and the adjacent peak separation (if any) desired. – hotpaw2 Apr 17 '20 at 00:31
@hotpaw2 Thanks! I now see what you mean – Tom Huntington Jun 27 '20 at 21:04
@DanBoschen You may like to read my edit – Tom Huntington Jun 27 '20 at 21:05
1

@TomHuntington Nice, too bad I can't upvote twice! – Dan Boschen Jun 27 '20 at 21:07
I tossed in a an upvote for you Dan. Technically speaking, broader than DSP, "Resolution" is based on the word "Resolve", which in practice means how close can two things get together before you can't tell them apart. With proper techniques (not talking windows), the resolution capability of a DFT is higher than the bin width, which is often called it's resolution, which I believe is the quoted question's intent. – Cedron Dawg Jun 27 '20 at 22:01
Theoretically, with infinite precision, two noiseless tones can be resolved until their parameters become equal. Practically speaking, noise will swamp any reasonable effort, so better to extend your frame or simply do envelope analysis in the time domain. – Cedron Dawg Jun 27 '20 at 22:01
@CedronDawg According to wikipedia: If the waveform under analysis comprises two sinusoids of different frequencies, leakage can interfere with our ability to distinguish them spectrally. Possible types of interference are often broken down into two opposing classes as follows: If the component frequencies are dissimilar and one component is weaker, then leakage from the stronger component can obscure the weaker one's presence. But if the frequencies are too similar, leakage can render them unresolvable even when the sinusoids are of equal strength. – Tom Huntington Jun 27 '20 at 22:25
Windows that are effective against the first type of interference, namely where components have dissimilar frequencies and amplitudes, are called high dynamic range. Conversely, windows that can distinguish components with similar frequencies and amplitudes are called high resolution. https://en.wikipedia.org/wiki/Window_function. The mainlobe width is related to the resolution, and the sidelobe height to the dynamic range – Tom Huntington Jun 27 '20 at 22:25
1

@TomHuntington Wikipedia apparently doesn't know about my formulas or techniques. I am still having difficulty with intrabin resolution (due to noise and the sensitivity of the equations), but nearby frequencies are resolvable by iterative estimation and removal. When you remove the large tone, the smaller one is estimable. When you remove the small tone, you get a better read on the large one. And so on, even with multiple tones. Any kind of window complicates the math. – Cedron Dawg Jun 27 '20 at 23:06
1

If you have two sinusoids of near equal amplitude, but very close in frequency, you can use the beat phenomenon in the time domain. The apparent frequency of the signal (by zero crossings) is the average of the two frequencies and the frequency of the envelope (if you take a full cycle, e.g. two lobes) is half the difference of the frequencies. – Cedron Dawg Jun 27 '20 at 23:12
1

Also, resolution defines your precision in whatever you are measuring. It says nothing about accuracy. – Cedron Dawg Jun 27 '20 at 23:14

score 4 · Answer 2 · answered Feb 01 '19 at 14:55

Depends a bit on what you are trying to achieve.

If you do an FFT of length $N$ of a signal sampled at sampled at a rate of $F_s$, then many people would say your frequency resolution is $\frac{F_s}{N}$. Whether that's correct or not, really depends on how exactly you define frequency resolution and what you are planning to do with it.

What's really happening is that you sample a frequency domain function with a sampling interval of $\frac{F_s}{N}$. As soon as you pick an FFT size, you are sampling in both domains with the sampling intervals being $\frac{1}{F_s}$ in time and $\frac{F_s}{N}$ in frequency.

Frequency domain sampling has all the same properties, requirements and problems as time domain sampling, you can get aliasing, you can interpolate, there is assumed periodicity in the other domain, etc.

By simply applying the sampling theorem we could argue that the frequency resolution required to fully characterize a signal is simply the inverse of the length in the time domain. This works well for signals that are inherently time bound, such as the impulse response of an LTI system.

However it's not practical for long continuous signals. In this case you need to pick a frequency resolution that's "good enough" for your application, and that really depends on the requirements and goal of your specific application.

score 4 · Answer 3 · answered Apr 16 '20 at 21:56

The binwidth of the FFT or the resolution of repreantation as I like to call it is Fs/N, where N is size of FFT. The actual resolution will depend on the window you use and the length of the window.

For ex: a rectangular window will provide maximum resolution but less dynamic range. Other more smoother windows provide less resolution with more dynamic range or lower side lobes.

Royi · Answer 4 · 2022-04-18T10:08:05.317

The Sampling is given by $ {T}_{s} = \frac{1}{2000} $ [Sec].
The Window length is 1000 Samples.
Since the Window length must be equal to the data length we infer the data length is 1000 samples which means the sampling time is $ 0.5 $ [Sec].

The bin width in the DFT is determined by the ratio between the number of samples in the DFT to the Sampling Frequency.
In your case the sampling frequency is $ {F}_{s} = 2000 [Hz] $ and the number of samples in the DFT is 2000. So the bin width is:

$$ \frac{{F}_{s}}{N} = \frac{2000}{2000} = 1 [Hz] $$

The resolution, in the sense of being able to see something without interference from other bins. This is basically the width of the main lobe of the DFT of the rectangle window (See DSP Related - Rectangular Window). The main lobe radius depends on the sampling interval which is $ 0.5 [Sec] $. For a given sampling frequency the more samples the higher resolution (Data samples and not DFT samples).

What is Frequency Resolution?

4 Answers4