I am unable to solve this question, 10.10 from GATE IN 2004 (a previous year question paper for an exam targeted at engineering graduates in India.)
So I tried to solve the 10.10 by considering the real frequency shift transformation's general form,
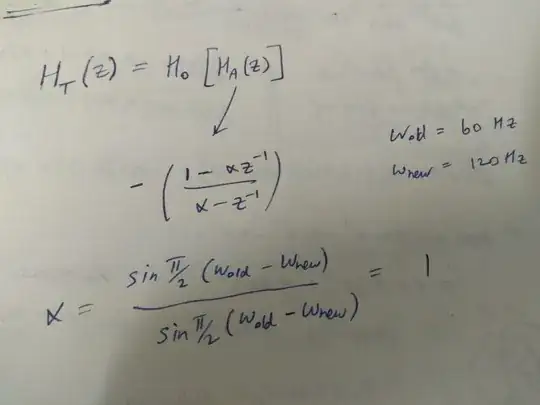
I am not getting any answer close to the options! I wonder what I am doing wrong.
So 1) what is the answer to the question 10.10 shown above?
2) how is this formula for the coefficient derived?
This is an allpass transformation, i.e., the unit circle is mapped to itself. On the unit circle we have
$$e^{-j\omega_0}=\frac{1-\alpha e^{j\hat{\omega}_0}}{e^{j\hat{\omega}_0}-\alpha}\tag{1}$$
For given values of $\omega_0$ and $\hat{\omega}_0$ you can compute $\alpha$ from $(1)$:
$$\begin{align}\alpha&=\frac{1-e^{-j(\omega_0-\hat{\omega}_0)}}{e^{j\hat{\omega}_0}-e^{-j\omega_0}}\\&=\frac{e^{-j(\omega_0-\hat{\omega}_0)/2}}{e^{-j(\omega_0-\hat{\omega}_0)/2}}\cdot \frac{e^{j(\omega_0-\hat{\omega}_0)/2}-e^{-j(\omega_0-\hat{\omega}_0)/2}}{e^{j(\omega_0+\hat{\omega}_0)/2}-e^{-j(\omega_0+\hat{\omega}_0)/2}}\\&=\frac{\sin\left(\frac{\omega_0-\hat{\omega}_0}{2}\right)}{\sin\left(\frac{\omega_0+\hat{\omega}_0}{2}\right)}\tag{2}\end{align}$$
With $\omega_0=2\pi\cdot 60/400$ and $\hat{\omega}_0=2\pi\cdot 120/400$ we get from $(2)$ the value $\alpha=-0.45965$.
