0

I have a signal (in blue) that I would like to smooth out (in red, moving average).

I would like to get red peaks to look more round than triangular and at the same time their width would become closer to the original ones.

enter image description here

Do you know / can you suggest a filter that would yield such result ?

Background:

The input is the zero-crossing rate from a song, for building a colored waveform as I've tried in this question : Coloring a waveform with spectral centroid or by other means

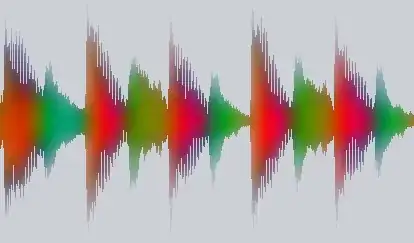
Here's the result of the new approach:

(unprocessed)

enter image description here

(ideal result, cheated somehow here using a post, expensive gaussian blur)

enter image description here

Update

Here's the result, using @Laurent Duval answer:

enter image description here

Also, I still need to try all of your suggestions again as my input/initial take was buggy, surprisingly now the ZCR yields better output than using FFTW out of the box (pics on the right):

enter image description here

Update 2

Simple moving average (green: 1-pass, gold: 2-passes)

enter image description here

Community
  • 1
Eric Cartman
  • 284
  • 1
  • 8

4 Answers4

3

Use two or three passes of moving average (can be pipelined).

  • This does not provide an answer to the question. To critique or request clarification from an author, leave a comment below their post. – jojeck Sep 15 '15 at 11:48
  • 2
    @jojek: I don't agree. –  Sep 15 '15 at 11:53
  • Going to give it a try and come back here. – Eric Cartman Sep 16 '15 at 03:44
  • See my update, basically it works but there's latency being introduced and original level is drastically reduced ... is there any way to overcome these two issues ? thank you. – Eric Cartman Sep 16 '15 at 07:18
  • You don't seem to have the latency problem in @Laurent Duval's solution. How come ? –  Sep 16 '15 at 07:35
  • Lowpass filtering indeed lessens the high frequencies. You can't achieve much better with a linear and simple filter. –  Sep 16 '15 at 07:40
  • I guess we hit the limits of the moving average for this specific issue. Thanks anyway. – Eric Cartman Sep 17 '15 at 07:32
2

I am not sure I understand "round" versus "triangular". Yet in chemistry, least-squares polynomial fitting filters are used to keep the smooth shape of spectra peaks. The most famous are the Savitzky–Golay filters. They have been revived in signal processing by a recent overview paper by R. W. Shafer: What Is a Savitzky-Golay Filter? (2011).

Laurent Duval
  • 31,850
  • 3
  • 33
  • 101
  • Well, I would like those red peaks to be wider than they are now, I guess they would look more round/sinusoid-like, if that makes sense ! Anyway, going to dig on your suggestion and come here for feedback, thank you ! – Eric Cartman Sep 14 '15 at 21:18
  • Your solution looks promising, I haven't coded the filter by myself but I think I've found a pretty good implementation based on "Numerical recipes in C" (http://altaxo.sourceforge.net/AltaxoClassRef/). Could you suggest some parameters regarding my update section in the question ? Basically, I would to keep each of the second bump to roughly the same level instead of being halved. Thank you ! – Eric Cartman Sep 16 '15 at 03:43
  • Thank you for the update, excellent news. As for the parameters, I do not have access to your sampling and signal properties, thus not able to have a guess. The definition and explanation of SG filters in Numerical Recipes is pretty good to, and might help you to this respect – Laurent Duval Sep 17 '15 at 05:54
  • Thank you, it does really address the initial concern, I'll read the article in detail. – Eric Cartman Sep 17 '15 at 07:30
1

Try a small Gaussian filter.

An approximation to the Gaussian can be achieved by applying a moving average filter multiple times.

geometrikal
  • 3,616
  • 15
  • 27
0

In the question Aybe implied that the red curve is a moving average of the blue curve. That doesn't look correct to me. (It seems to me that a moving-averaged output would not have the sharp peaks seen in the red curve.) My first thought was to suggest, as Yves Daoust did, a moving average filter as a possible answer to the question. If Yves and I had access the the blue curve's sample values we could see if a true moving average filter will satisfy Aybe.

Richard Lyons
  • 5,777
  • 13
  • 25