Frequency response of FIR (MTI delay line canceller) with non constant period

Question

Short question

How to plot the magnitude of frequency response of the delay line canceller with non constant period using GNU Octave? Or more directly: how to plot magnitude of frequency response of staggered PRF (pulse repetition frequency) MTI (moving target indicator) processors?

Full question

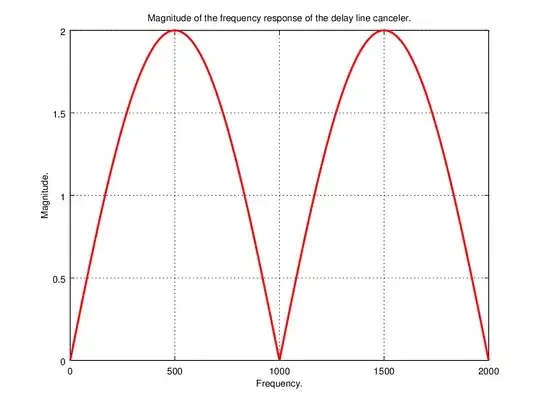
I try to plot magnitude of frequency response of the MTI delay line canceller (some kind of FIR) which has the following structure using GNU Octave:

structure of the delay line canceller

With tips in my related post I can plot frequency response for constant period:

close all;
clear all;

T   = 1e-3;
f   = linspace (0, 2 / T, 1000);
w   = 2 .* pi .* f;
z   = exp (-j .* w .* T);
H_z = 1 - z .^ -1;

plot (f, abs (H_z), 'r', "linewidth", 2);
hold on;
grid on;
title ("Magnitude of the frequency response of the delay line canceler.");
xlabel ("Frequency.");
ylabel ("Magnitude.");

enter image description here

But now I am interesting in frequency response for non constant period:

determinate values of period;
random values of period.

I try to do in the following way:

close all;
clear all;

T_1   = 0.001;
T_2   = 0.0012;
f     = linspace (0, 2 / min (T_1, T_2), 1000);
w     = 2 .* pi .* f;
z_1   = exp (-j .* w .* T_1);
z_2   = exp (-j .* w .* T_2);
H_z_1 = 1 - z_1 .^ -1;
H_z_2 = 1 - z_2 .^ -1;
k     = 1 / 2;
H_z   = k .* (H_z_1 + H_z_2);

plot (f, abs (H_z), 'r', "linewidth", 2);
hold on;
grid on;
title ("Magnitude of the frequency response of the delay line canceler for alternate values of period T1 and T2.");
xlabel ("Frequency.");
ylabel ("Magnitude.");

enter image description here

Another words, I mean that: common frequency response is the normalized sum of the frequency response for each value of the period.

Am I right? If yes, is this approach will be correct for random values of period?

Notes

Here is some related papers, when mentioned frequency response of staggered PRF MTI processors:

first (Pg 66 in books numeration or 81 in pdf-document numeration);
second (Pg 32).

So, do you have any clear frequency response expression, with time varying parameters, in order to be reproduced? Similar to the sine absolute value for the previous filter? — Brethlosze, Dec 25 '16 at 22:59

score 2 · Accepted Answer · answered Mar 21 '15 at 18:54

If you mean that you want a time-varying delay then the whole system becomes time-varying, which means that there is no such thing as a frequency response in the conventional sense. Only linear time-invariant systems can be described by a frequency response. There are of course ways to describe time-varying systems, but the question is what it exactly is that you expect from such a description of the system. What you've done in your example is subtract two delayed signals from the original signal, which is in fact a time-invariant system. In sum, what you're looking for (a frequency response description of a system with a time-varying delay) does not exist.

Thanks for your answer (and patient)! I have updated my question (change Short question and add Notes at the end). So now I know that what I am interesting in is called: Frequency response of staggered PRF (pulse repetition frequency) MTI (moving target indicator) processors. May be my question is improperly and I hope that this additional information clarify it. — Gluttton, Mar 21 '15 at 22:32

Frequency response of FIR (MTI delay line canceller) with non constant period

1 Answers1