Derivative of noisy signal

Question

My input signal is phase vector. I want to differentiate it to get frequency vector. My input signal is somewhat noisy. Here is the input signal.

This is the derivative of the input signal as calculated using

diff(inputSig)

When i differentiate this signal, I am not getting a smooth curve. The output looks 'spikey'. I am guessing it is because of the noise in the input signal (is this 'derivative kick'?). How to avoid this and get a smooth derivative curve?

Answer 1

2 point discrete differentiation is bound to produce highly noisy results. try the 5-points stencil. you can also generate coefficients (i.e. more points) yourself using derivation of Lagrange polynomials.

Answer 2

Look into the "Savitsky Golay Differentiation Filter"

Answer 3

You can find the wavelet transform, and use derivatives of wavelets. In this spirit, there is a procedure to directly calculate derivatives based on them.

The beauty of the wavelet transform is that you should be able to discard high-frequency components, theoretically coming from the underlying noise and sampling rate.

If you can get your hands on this and this, for example, you should be able to apply them.

Answer 4

Try boxcar line fitting with different length of times. This method filters and smooths the derivative

Answer 5

You can apply the concept of "scale" to your original data. The original data can be considered at the "finest" or "smallest" scale in the sense that all details are available to you. But you might not be interested in this level of detail since it might have noise that is affecting you.

If you convolve your original data with a Gaussian (normalized) of a given size, then you are effectively smoothing your signal and looking at a "larger scale". By choosing different "sigma" (width) of your gaussian, you can smooth your signal, hence its derivative.

You could start with a small sigma of 5-10 and see if the smoothing is sufficient for you.

Answer 6

To get a numerical derivative of inputSig, we should do something like (python code):

import pandas as pd
DF = pd.DataFrame
def derivative(X,Y,n=1):
    '''Central finite difference derivative of Y with respect to X, n points appart from central.'''
    if len(X) != len(Y) : raise Exception ( 'X, Y must have equal lengths...')
    n = int(n) # n must be integer
    if n == 0 : n = 1 # n must be greater than 0
    d = DF()
    d['X'],d['Y']=DF(X),DF(Y)
    YF,YR,XF,XR = d.Y.diff(n),d.Y.diff(-n),d.X.diff(n),d.X.diff(-n)
    return (YF-YR)/(XF-XR)
dt = 1 # time increment definition for evenly stepped inputSig
y = inputSig
t = pd.array(range(len(inputSig)))*dt # evenly sampled y with time (at dt intervals)
dydx1 = derivative(t,y,1) # noisy derivative
dydx3 = derivative(t,y,3) # lower noise, but more derivative distortion

Central differences, as defined above, are better than forward schemes; and do not worry with initial and final nans. Note that increasing n in derivative reduces noise but also distorts the derivative at low frequencies. With a spiky derivative, you should consider increasing precision of phase measurements, or alternativelly, pass the derivative through a low frequency filter and integrate the filtered derivative to reconstruct the signal (must add a constant after all, to allow its adjustment to the noisy original signal). Note also that differentiating a noisy signal increases the noise, but integrating (pandas DF.cumsum() for instance, and must consider dt increments also) reduces it, so that it is easier to perform noise reduction on the derivative and then integrate it to get a less noisy signal, at least from my point of view.

Answer 7

The problem is that numerical differentiation is considered an ill-posed problem because a small change in the input parameters results in big changes at output. Using other schemes, such as centred differences, instead of progressive differences might give you slightly better results, but it does not solve the issue.

There are multiple ways to solve this, apart from the ones answered by other users. Let me show you some of them, ordered from simpler to more complex.

In all the examples I am using $f(x) = \cos^2(x) + \sin(x) + \epsilon (x)$ as the function that I want to take the derivative of (where $\epsilon (x)$ is a small error, $|\epsilon (x)| < 0.01$). The derivative should be $f'(x) = - 2 \cos(x) \sin(x) + cos(x)$, but I won´t get that result a priori because of the noise.

1. Approximate the function to $g(x)$. Being $g(x)$ smoother. Polynomial fitting, for example. You can also use least-squares method to approximate the function to a non-polynomial.

For example, I will use, $g(x) = a_0 + a_1 sin(x) + a_2 cos(x) + a_3 sin(2x) + a_4 cos(2x)$. Here is the code in MATLAB:

A = [ones(size(x,2), 1), sin(x'), cos(x'), sin(2*x'), cos(2*x')];
A_sist = A'*A;
b_sist = A'*y_noised;
sol = A_sist\b_sist;
y_fitted = sol(1) + sol(2)sin(x) + sol(3)cos(x) + sol(4)sin(2x) + sol(5)cos(2x);

2. Add a term that penalizes strong changes in the derivative.

Instead of computing the derivative at each point, $d_0, d_1, ..., d_{n-1}$ as

$d_k = \frac{f_{k+1}-f_k}{\Delta x}, \;\; x=0,...,n-1$

compute them such that the function

$F_1(d_0, ..., d_{n-1}) = \sum_{k=0}^{n-1}\left(d_k - \frac{f_{k+1}-f_k}{\Delta x}\right)^2 + \alpha \sum_{k=0}^{n-2}\left(\frac{d_{k+1}-d_k}{\Delta x}\right)^2 $

is minimized. $\alpha$ is a penalty term, that shouldn’t be too hight to avoid over-regularization. The minimum is obtained when $\delta F_1 / \delta d_0 = \delta F_1 / \delta d_1 = ... = \delta F_1 / \delta d_n = 0 $. If you take a piece of paper and a pencil you should be able to compute those derivatives and write it all as a linear system of equations. We obtain the following system:

$ A D = B $

Where $B = (b_0, b_1, ..., b_n)^T; \;\; b_k = (f_{k+1} - f_k)/\Delta x $, $D = (d_0, d_1, ..., d_{n-1})$, and $A = I + \frac{\alpha}{(\Delta x)^2} A_1$. $A_1$ is a tridiagonal matrix where the main diagonal is $(-1, 2, ..., 2, -1)$ and the two other diagonals have $-1$ everywhere.

The cool thing is that now A is a well-conditioned matrix, so you won´t get big variations in the solution when there are small variations in the function.

3. Write the problem as a linear system and use Tikhonov or Landweber method to regularize it.

We are looking for $D(x) = f'(x)$. We know that if $f(x)$ is continuous,

$ \int_{x_0}^{x} D(t) dt = \int_{x_0}^{x} f'(t) dt = f(x) - f(x_0) $

Let $g(x) = f(x) - f(x_0)$. You can aproximate the integral $\int_{x_0}^{x_k} D(t) dt = g(x_k)$ using the trapezoidal rule:

$ \int_{x_0}^{x_k} D(t) dt \approx \frac{\Delta x}{2} \left( D(x_0) + 2 \sum_{j=1}^{k-1} D(x_j) + D(x_k) \right) $

If we call $d = (D(x_0), ..., D(x_{n-1})$ and $g = (g(x_0), ..., g(x_{n-1})$, then, we end up with a linear system of the form $A d = g$, that can be solved using some regularization algorithm.

I won´t show the entire procedure because it is quite long, but here are the results I got with Tikhonov:

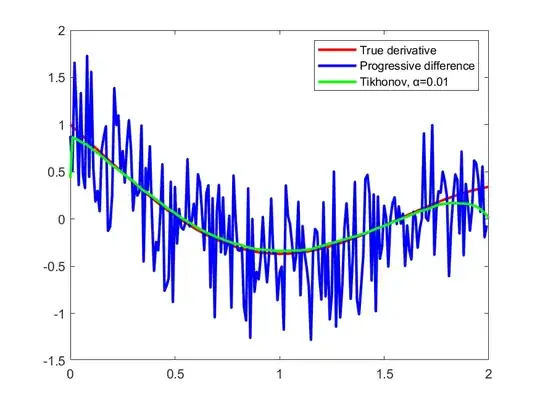
And here are the results I got with Landweber:

I hope this helped.