Fitting a psychometric function when data does not lend itself to a sigmoidal fit

Question

I'm fitting a psychometric function to a range of data. The majority of this data lends itself to a sigmoidal fit (i.e. participants can do the task), but some individuals are absolutely unable to do the task. I'm planning to compare the slopes obtained from different conditions, but I've hit a wall with the unable-to-do-the-task data.

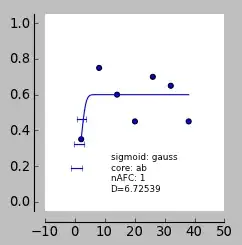
Fitting a function to this data, the slope should be nearly flat, right? However, the data is really noisy and some weird fitting is occurring - I end up getting erroneously high slopes. I'm using pypsignifit, the parameters I'm using can be seen below. Any idea how to stop this happening?

num_of_block  = 7
num_of_trials = 20

stimulus_intensities=[3, 7, 13, 20, 27, 32, 39] # stimulus levels
percent_correct=[.38, .75, .6, .43, .7, .65, .43]     # percent correct sessions 1-3
num_observations     = [num_of_trials] * num_of_block      # observations per block
data= np.c_[stimulus_intensities, percent_correct, num_observations]
nafc = 1
constraints = ('unconstrained', 'unconstrained', 'unconstrained', 'Beta(2,20)' )
boot = psi.BootstrapInference ( data, core='ab', sigmoid='gauss', priors=constraints, nafc=nafc )
boot.sample(2000)
print 'pse', boot.getThres(0.5)
print 'slope', boot.getSlope()
print 'jnd', (boot.getThres(0.75)-boot.getThres(0.25))

Answer 1

What you are looking for is called Hierarchical, Multi-level or Random-effects model. In your particular case the solution is a hierarchical logistic regression.

Assume $y_{st} \in \{0,1\}$ is the response of subject $s$ on trial $t$ and $x$ is the dependent variable then a simple hierarchical model that solves your problem is:

$y_{st}\sim \mathrm{Bernoulli}(\mathrm{logit}(\alpha_s+\beta_s x))$

$\beta_s \sim \mathcal{N}(\mu,\sigma)$

where $\mu$ is the population value of the slope and $\beta_s$ is the subject level estimate. Roughly, $\mu$ is a weighted average of all $\beta_s$ where the weight of each $\beta_s$ is inversely proportional to the variance of the estimate of $\beta_s$. For more details on hierarchical logistic regression and for extensions of the simple model, that I have suggested above, refer to Chapter 14 in Gelman & Hill (2006).

Fitting a function to this data, the slope should be nearly flat, right?

No. The slope should be uncertain. Flat slope looks differently, say $(10,0.61), (20,0.59),(30,0.6),(40,0.58),(50,0.6)$. The corresponding estimate of $\beta$ should show wide interval such that you can't conclude that $\beta>0$ or $\beta<0$ or $\beta=0$ (as you suggested).

How will a hierarchical model handle such uncertain $\beta_s$? This $\beta_s$ will contribute little to the estimate of $\mu$. Instead $\beta_s$ for this particular subject will be pulled towards $\mu$. The hierarchical model will effectively tell you that if your data is inconclusive, it will just assume that the subject is a typical member of the population (that is if $\mu$ had been estimated reliably) and discard the erratic data.

Literature: Gelman, A., & Hill, J. (2006). Data analysis using regression and multilevel/hierarchical models. Cambridge University Press.

Answer 2

At the heart of the matter is the fact that 60% "yes" responses independent of the stimulus level (i.e., the problematic data) can arise from both an extremely sensitive subject (i.e., steep slope) with a moderate bias and a high lapse rate and an extremely insensitive subject (i.e., shallow slope) with a moderate bias and a low lapse rate. For your data the steep slope/high lapse rate fit is slightly better than the shallow slope/low lapse rate when your prior on the lapse rate is based on a Beta distribution. My guess is if you used a uniform prior on the lapse rate, and possibly on the guessing rate, this will result in the shallow slope fit being better. I would try something like "Uniform(0,0.1)".