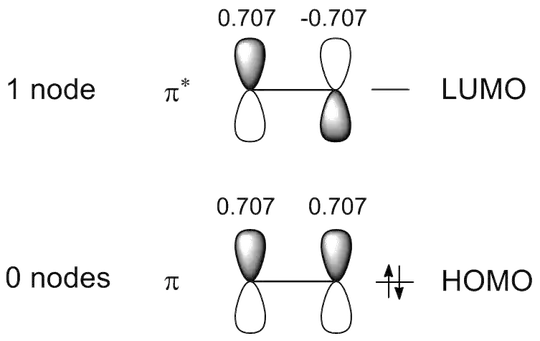11

I asked a question previously about "why" it is the case the expanding the size of pi-conjugated systems decreases the required energy to excite an electron from a HOMO to a LUMO band: Why does the energy gap for π - π* transitions shrink with the size of the pi-conjugated system?. The user "Philipp" (and others) very patiently and kindly explained the reason for this by pointing out the expansion in the number of possible bonding and anti-bonding configurations for a polymethine-like pi-conjugated system.

However, there's something I'm missing that has to do with what is probably my lack of knowledge about chemistry. If we look at this image: https://i.stack.imgur.com/Ti3cx.png (provided by "Philipp") why is that that we have an energy gap between $\Psi_2$ and $\Psi_3$ smaller than the energy gap for a simpler, smaller pi-conjugated system where the HOMO corresponds to a single pair of p-orbitals in a bonding conformation and the LUMO corresponds to the same single pair of p-orbitals in an anti-bonding conformation (i.e. this system: https://i.stack.imgur.com/9cscv.png)?

My guess that this would be because the bonding interactions that exist in the larger pi-conjugated system mitigate the penalty for having the one anti-bonding interaction?

Update --- Could we justify the above guess using something like an overlap integral (if we know the shape of the two bonded p-orbitals forming a pi-bond)? If so, this would be quite intuitive.

Community
  • 1
user4717
  • 477
  • 1
  • 4
  • 9
  • 1
    Luckily enough, you have chosen one of very first studied problems in theoretical chemistry. Have a look here: http://en.wikipedia.org/wiki/Hückel_method – ssavec Mar 05 '14 at 07:19
  • I can only second ssavec. HMO is the way to go. Does your library carry a copy of The HMO model and its application by Edgar Heilbronner and Hans Bock? – Klaus-Dieter Warzecha Mar 05 '14 at 07:25
  • @KlausWarzecha I wish I had easy access to that text. Is it good enough to be worth purchasing? – user4717 Mar 05 '14 at 07:33
  • Just the 1st of three volumes is between USD 70 and 250 for a used copy on amazon! Volumes 2 and 3 are exercises and tables, resp. Are you sure that you'll be using it in 2-5 month? Might be better to save the money and use free online resources from universities. Pesonally, I wouldn't buy it. – Klaus-Dieter Warzecha Mar 05 '14 at 07:59

2 Answers2

13

If you want to really understand why energy levels of conjugated $\pi$ systems are the way they are I suggest you take a good look at the Hückel theory as @ssavec suggested - this method is only an approximation but because of its simplicity it is really good for helping you to understand the underlying concepts. Nevertheless, doing as you suggested and looking at the overall overlap between the $\text{p}$ orbitals in a given molecular orbital does indeed seem to work although I don't have a strict justification for that.

From Hückel theory it is known that the coefficients of the $\text{p}$ orbitals in a given molecular orbital can be calculated as

\begin{equation} c_{j,r} = \sqrt{\frac{2}{N + 1}} \sin\Bigl(\frac{r j \pi}{N + 1}\Bigr) \end{equation}

giving the coefficient $c_{jr}$ for atom $j$ in molecular orbital $r$ of a conjugated system of $N$ atoms (so that $j$ and $r = 1, 2, 3, \dots , n$).

Let's apply this to butadiene.

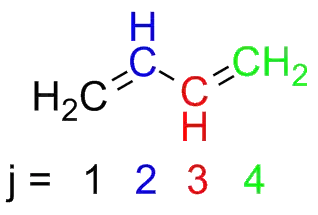
The $\pi$ molecular orbitals of butadiene are $\Psi_{1}$, $\Psi_{2}$, $\Psi_{3}$, and $\Psi_{4}$. They are built from a linear combination of 4 atomic $\text{p}$ orbitals ($\phi_{1}$, $\phi_{2}$, $\phi_{3}$, and $\phi_{4}$), so

\begin{equation} \Psi_{r} = c_{1,r} \phi_{1} + c_{2,r} \phi_{2} + c_{3,r} \phi_{3} + c_{4,r} \phi_{4} \end{equation}

When you calculate the atomic orbital coefficients for each molecular orbital $r$ then you get to the following picture:

enter image description here

where the numbers above the different $\text{p}$ orbitals are the coefficients.

Doing the same for ethene you get the following:

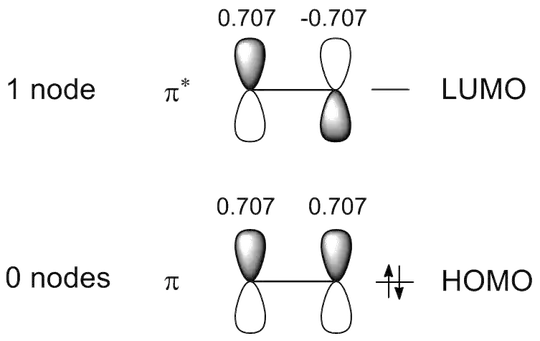
Now, you need to compare the overall overlap in the HOMOs of ethene and butadiene. Since it is already assumed in the Hückel theory only the overlap between neighboring $\text{p}$ orbitals is considered. Furthermore, it is useful to set the overlap integral of two "normal" $\text{p}$ orbitals (both with coefficient $c = 1$) to 1 (its exact value doesn't matter because only the relative amounts of overlap in different MOs are important for this comparison), so that you can calculate the overall overlap in a molecular orbital simply by multiplying the coefficients of neighboring $\text{p}$ orbitals and summing over these products. So, for the overlap in the ethene and butadiene HOMOs you get:

\begin{align} S_{\text{HOMO, ethene}} &= 0.707 \cdot 0.707 \\ &= 0.500 \\ \\ S_{\text{HOMO, butadiene}} &= 0.600 \cdot 0.371 + 0.371 \cdot (-0.371) + (-0.371) \cdot (-0.600) \\ &= 0.307 \end{align}

There is less overlap and thus less bonding in the HOMO of butadiene than in the HOMO of ethene which would imply that the HOMO of butadiene is higher in energy than that of ethene.

Now, what about the LUMOs:

\begin{align} S_{\text{LUMO, ethene}} &= 0.707 \cdot (-0.707) \\ &= -0.500 \\ \\ S_{\text{LUMO, butadiene}} &= 0.600 \cdot (-0.371) + (-0.371) \cdot (-0.371) + (-0.371) \cdot 0.600 \\ &= -0.307 \end{align}

There is more overlap and thus more bonding (or better to say less antibonding) in the LUMO of butadiene than in the LUMO of ethene which would imply that the LUMO of butadiene is lower in energy than that of ethene.

So, the HOMO of butadiene is higher in energy than that of ethene and the LUMO of butadiene is lower in energy than that of ethene. Thus, the HOMO-LUMO gap in butadiene is smaller than that in ethene.

Philipp
  • 17,748
  • 4
  • 79
  • 118
  • I was hoping I'd see a more mathematical description like this in the other question. Great work! – Nicolau Saker Neto Mar 05 '14 at 13:21
  • 1
    @NicolauSakerNeto Thanks. As for the other question: I had the feeling that the OP wanted something intuitive rather than mathematical that's why I gave a very pictorial description in terms of in-phase and out-of-phase combinations in the first place. But I think about adding another answer with a full mathematical treatment of the Hückel model if I find the time (and motivation :)). – Philipp Mar 05 '14 at 13:29
  • Very sweet graphics! – tschoppi Mar 05 '14 at 13:35
  • @tschoppi ChemDraw magic :) – Philipp Mar 05 '14 at 13:40
  • @Philipp Actually I'm fairly certain this is more a case of Philipp magic. – user4717 Mar 05 '14 at 17:49
  • Amazing answer! – Yusuf Hasan Nov 20 '19 at 18:36
  • @Philipp Indeed a great answer! Would you mind add the general mathematical expresion (in Hückel's theory) that shows that increasing the conjugation decreases the HOMO-LUMO gap? – ado sar Jan 06 '20 at 16:32
8

Here's an alternate approach to answering this question using the "Particle in a Box" approach. The $N^{th}$ energy level for a particle in a one-dimensional box is given by $$E_n=\frac{n^2h^2}{8mL^2}$$ where h is Planck's constant, m the mass of the particle and L the length of the box. The energy of the N+1 energy level is equal to $$E_{n+1}=\frac{(n+1)^2h^2}{8mL^2}$$. Subtracting these two terms gives us the energy separation between these two energy levels as $$\Delta E=\frac{(2n+1)h^2}{8mL^2}=K\frac{2n+1}{L^2}$$. Pictured below is the beginning of our polyene series, ethylene, butadiene, hexatriene...

enter image description here

For simplicity, let's assume all bond lengths are equal. Then the "length" of our box increases by 2L each time we move from ethylene to butadiene to hexatriene, etc. If we now compare the difference of the $\Delta E's$ (the $\Delta\Delta E's$) for the $N^{th}$ and $(N+1)^{st}$ energy levels between ethylene and butadiene, we find that the difference in energy level separation is given by $$\Delta\Delta E=K(2n+1)(\frac{1}{L^2}-\frac{1}{9L^2})= K'(\frac{8}{9L^2})$$ If we perform the same comparison for butadiene and hexatriene we see that $$\Delta\Delta E=K(2n+1)(\frac{1}{9L^2}-\frac{1}{25L^2})= K'(\frac{16}{225L^2})$$ and for hexatriene compared to octatetraene it is $$\Delta\Delta E=K(2n+1)(\frac{1}{25L^2}-\frac{1}{49L^2})= K'(\frac{24}{1225L^2})$$ In other words as we increase the length of our box (increase the length of our polyene), the energetic separation between any corresponding pair of energy levels (HOMO-LUMO being one case) will shrink. Hope this helps!

ron
  • 84,691
  • 13
  • 231
  • 320
  • +1, retreating to those simple model systems is very useful for getting an idea of the general behavior. – Philipp Mar 05 '14 at 15:07
  • 1
    @Philipp Thank you. Over the years I've learned that some people will see the answer more clearly with one approach, other folks will see the answer more easily with another approach. So presenting different ways to arrive at an answer is always helpful. – ron Mar 05 '14 at 16:16
  • @ron This is really getting close to an explanation that makes complete sense to me. However, how do we understand the above "Particle in a Box" system at the limit of an ultra-large pi-conjugated system? I.e. for $(D = 1)$ a $k$-unit polyene chain as $k \to \infty$, for $(D = 2)$ graphene, and for $(D = 3)$ a metal like Cu? Regarding the $D = (2,3)$ scenarios I just outlined, I understand the expression above is for the $(D = 1)$ case only, but nevertheless, does this question make sense? – user4717 Mar 05 '14 at 17:42
  • An example of an ultra-large pi-conjugated system would be polyacetylene and other similar molecules. In such a case the "Particle in a Box", as well as other MO approaches, tells us that our discrete energy levels bur into a continuum (what's called a "band") with a small band gap between the occupied band (valence band) and unoccupied band (conduction band). So in effect our system has become a quasi-metal, and begins to behave like a metal. It becomes more like a conductor and less like an insulator. If you "Google" "particle in a 2 (or 3) dimensional box", you'll find that – ron Mar 05 '14 at 18:15
  • the solution is analogous to our 1-dimensional solution. Instead of a $1/L^2$ term, we now have $1/L^2, 1/W^2 and 1/H^2$ terms – ron Mar 05 '14 at 18:17
  • @ron That makes good sense to me, however, we should still have a reasonably large band-gap in a metal right (consider the photoelectric effect)? The above expression would appear to indicate that there should be a band gap of size zero as $L \to \infty$? Or am I not thinking correctly about the nature of the band gap in a metal / pseudo-metal? – user4717 Mar 05 '14 at 18:17
  • If I recall correctly, the PE effect knocks an electron out of the metal. That's not what we're doing, we're just promoting an electron, not effecting ionization. Thermal energy should be enough to allow an electron to be promoted from the valence band to the conduction band in a metal. But you are right about the band gap shrinking as the box size increases. However crystal defects, impurities, etc. often serve to limit the size of our box. That's why semiconductors are prepared under such stringent conditions - trying to make the box bigger, trying to make conduction easier. – ron Mar 05 '14 at 18:23
  • @ron Ok, that makes sense. So in a metal, there is no HOMO / LUMO gap, and we need to think about the "band gap" as corresponding to some exciton binding energy (i.e. the energy to split an electron and a hole). – user4717 Mar 05 '14 at 18:30
  • @user4717 Yes, that's my understanding – ron Mar 05 '14 at 19:11
  • However, the relation $\Delta E = K\frac{2n+1}{L^2}$ only shows the energy gap for transition with same quantum numbers. But the HOMO for a compound A (might be for n=2) whereas for a compound B (might be for n=3). It isn't guaranteed just by the increasing length. – ado sar Jan 13 '20 at 12:09