How to calculate the height of an hcp lattice?

Question

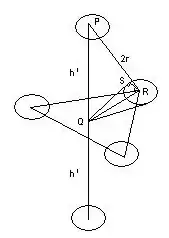
A hexagonal closed packing (hcp) unit cell has an ABAB type of packing. For calculating the packing fraction we require the volume of the unit cell.

Volume of hcp lattice = (Base area) $\cdot$ (Height of unit cell)
Each hexagon has a side = $2\cdot r$
Base area = $6$ (Area of small equilateral triangles making up the hexagon)
$$=6 \cdot \frac{\sqrt{3}}{4}\times(2r)^2$$ $$=6 \cdot \sqrt{3} \cdot r^2$$

Hence, volume $= 6 \cdot \sqrt{3} \cdot r^2 $ (Height of unit cell)

This is the point where I am stuck. How do I find out the height of the unit cell?

I searched in textbooks and found out that height $= 4r \cdot \sqrt{\frac{2}{3}}$. Can you please explain why is this so?

Answer 1

To calculate the height of a unit cell, consider a tetrahedral void in an hexagonal closed packing arrangement. It can be imagined as a 3 solid spheres touching each other and at the center-point, you have another sphere stacked over them. An interactive version can be viewed on this site. The situation looks like this:

If you join the centers of these four spheres, you'll get a tetrahedron. That's basically a pyramid with a triangular base. I'm assuming each edge of our tetrahedron to be equal to $a$.

Now, you have a pyramid ($ABCD$), with an equilateral base ($\Delta BCD$), I would like you to drop a perpendicular from the highest point ($A$) to the center ($G$) triangular base. If you're following me correctly, you'll have a figure like this:

All we have to do now is to calculate the length $AG$. For this, simply use the Pythagorean theorem in $\Delta AGD$.

$$ \begin{align*} AD^2 &= AG^2 + GD^2 \tag{1} \end{align*} $$

Although we know that $AD=a$, the side $GD$ remains unknown. But that's easy to calculate. The point $G$ is the centroid of $\Delta BCD$. Thus, the length $GD$ equals $a/\sqrt{3}$. Pluggging in the values in our first equation, we get $AG=a \sqrt{\frac{2}{3}}$. But note, this is half the height of our unit cell. Thus, the required height is $2a \sqrt{\frac{2}{3}}$.

Answer 2

We shall try it using the similarities between hcp and ccp. Here, we know that $hcp$ and $ccp$ have similar lattice except the fact that $hcp$ is ABAB type whereas $ccp $ is ABCABC type. Hence we also know that their packing fraction $(\phi) $ is same and $$\phi = \frac{\pi} {3\sqrt{2}}$$ Now as you mentioned Volume of hcp lattice $= 6\sqrt{3} r^2h$. There are 6 atoms in total in hcp. Hence $$\frac{6\left(\frac{4}{3}\right) \pi r^3}{6\sqrt{3} r^2 h} = \frac{\pi} {3\sqrt{2}}$$ Simplifying this we obtain the height of hcp lattice $$h=4r\left(\sqrt{\frac{2}{3}}\right)$$

Answer 3

In the hexagonal closest-packed structure, $a = b = 2r$ and $c = 4 \sqrt{\frac23 }r$, where $r$ is the atomic radius of the atom. The sides of the unit cell are perpendicular to the base, thus $\alpha = \beta = 90^\circ$.

For a closest-packed structure, the atoms at the corners of base of the unit cell are in contact, thus $a = b = 2 r$. The height ($c$) of the unit cell, which is more challenging to calculate, is $c = 2a \sqrt{\frac23} r = 4 \sqrt{\frac23} r$.

Let the edge of hexagonal base equal $a$

And the height of hexagon equal $h$

And radius of sphere equal $r$

The centre sphere of the first layer lies exactly over the void of 2nd layer B.

The centre sphere and the spheres of 2nd layer B are in touch

So, In $\Delta PQR$ (an equilateral triangle):

$\overline{PR} = 2r$, Draw $QS$ tangent at points

$$∴ \text{In } \Delta QRS\text{: } \angle QRS = 30^\circ, \overline{SR} = r$$

$$\cos30^\circ = \frac{\overline{SR}}{\overline{QR}}$$

$$\overline{QR} = \frac{r}{\frac{\sqrt{3}}{2}} = \frac{2r}{\sqrt 3}$$

$$∴ \overline{PQ} = \sqrt{\overline{PR}^2 - \overline{QR}^2} = \sqrt{4r^2 - \frac{4r^2}{3}}$$

$$h_1 = \sqrt{\frac{8r^2}{3}} = 2 \sqrt\frac{2}{3} r$$

$$∴ h = 2h_1 = 4 \sqrt{\frac23} r$$

Hence, in the calculation of packing efficiency of hcp arrangement,the height of the unit cell is taken as $4r\sqrt{\frac{2}{3}}$.

FROM