Rate-limiting in transition state theory

Question

Suppose an initial state $A$ can transition to either state $C$ or state $D$. Suppose further that both of these two processes are rate-limited by a transition to the same intermediate state $B$, as follows:

Note that $\Delta G_{AB}> \Delta G_{BC}>\Delta G_{BD}$.

According to transition state theory, rates are determined by the rate-limiting step. So the rate of each process will be the same,

\begin{align} r_{A\to C}&=r_{A\to B} \\ r_{A\to D}&=r_{A\to B} \end{align}

from which it follows that the number of transitions made during some large $\Delta t$ will also be the same,

\begin{align} N_{A\to C}&=r_{A\to B}\Delta t \\ N_{A\to D}&=r_{A\to B}\Delta t \end{align}

However, if we were to consider the two pathways collectively then we would predict more transitions to be made to state $D$ than $B$ since $\Delta G_{BD}<\Delta G_{BC}$.

How do we resolve this apparent discrepancy?

Answer 1

In transition state theory (TST, goldbook) one of the necessary assumptions is that reactants and products are in equilibrium. In principle this gives us \begin{align}\ce{ A &<=> [AB]^{$\ddagger$} -> B\\ B &<=> [AB]^{$\ddagger$} -> A\\ A &<=> B, }\end{align} and in addition to this, also \begin{align}\ce{ B &<=> [BC]^{$\ddagger$} -> C & B &<=> [BD]^{$\ddagger$} -> D\\ C &<=> [BC]^{$\ddagger$} -> B & D &<=> [BD]^{$\ddagger$} -> B\\ B &<=> C & B &<=> D, }\end{align} as well as \begin{align}\ce{ C <=> [BC]^{$\ddagger$} -> & B <=> [BD]^{$\ddagger$} -> D\\ D <=> [BD]^{$\ddagger$} -> & B <=> [BC]^{$\ddagger$} -> C\\ C <=> & B <=> D, }\end{align} and $$\ce{ C <=> A <=> D\\ [AB]^{$\ddagger$} <=> [BC]^{$\ddagger$} <=> [BD]^{$\ddagger$} }.$$

You can use TST to estimate rate constants. $$k = \frac{\mathcal{k}_\mathrm{B} T}{\mathrm{h}} \exp\left\{ −\frac{\Delta^\ddagger{}G^\circ}{\mathcal{R} T}\right\}$$

Since all components have to be in equilibrium, you can predict a ratio between them via Boltzmann statistics, hence: $$\frac{N([BC]^{\ddagger})}{N([BD]^{\ddagger})} = \exp\left\{ −\frac{\Delta^\ddagger{}G^\circ([BC]^{\ddagger})-\Delta^\ddagger{}G^\circ([BD]^{\ddagger})}{\mathcal{R} T}\right\}=\frac{N(C)}{N(D)} $$

The preceding equilibrium does not need to be considered to determine the ratio of the products. However, it is important to note, that there are many assumptions necessary for TST to work. For example, at higher temperatures, anharmonic corrections have to be considered. More crucial is the assumption, that the transition can be described as a translatory movement, i.e. it is treated with classical mechanics.

For a system with a preceding equilibrium, it is well possible, that the TST approximation breaks down completely.

Answer 2

On remark: just because activation energy high/low it doesn't necessarily mean that reaction is slow or fast. You cannot tell this without the pre-exponential factor.

The answer: Off course, the original statement should not applied as you do it. "According to transition state theory, rates are determined by the rate-limiting step." doesn't mean automatically that all the reaction rates are equal.

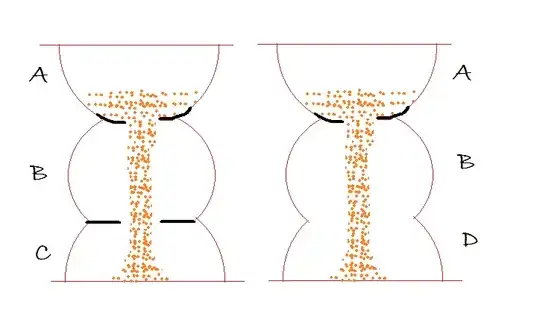
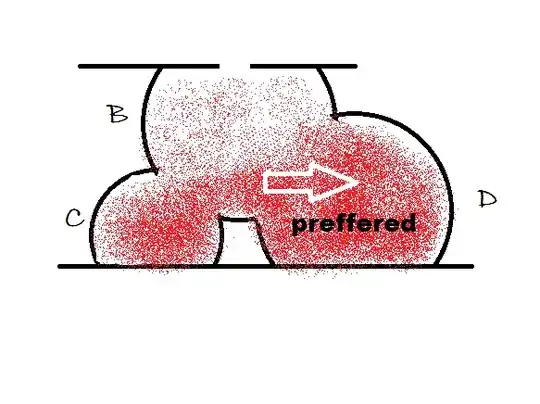
A to B conversion is slow compared to other processes, is true, but still B to C and B to D are competing processes. The original statement only means that B will not build up in bigger quantities, so during the reaction all the final products (C and D together) are approximately equal with the used A after you consider stoichimetries.

Edited for clarification (sorry, pretty new to LaTex):

You should consider all the transformations as independent equations. Black magic is not involved, "rate determining step" and such only helps making approximations so one can solve the coupled differential equations on napkin.

Example 1.

Let us assume a reaction system with $A \to B \to C$. The kinetics of the system can be describe by two independent equations

$A \to B$ with a corresponding $k1$ and $B \to C$ with a corresponding $k2$

To describe conversions we can get different equations:

$$ \frac{d[A]}{dt} = -k1 [A] $$

$$ \frac{d[B]}{dt} = k1 [A] - k2 [B]$$

$$ \frac{d[C]}{dt} = k2 [B] $$

We see that it is already pretty messy, so assumptions like $k1 << k2$ can help. The general way is that we say, this difference in the rate constants allows us to asume $$ \frac{d[B]}{dt} \approx 0 $$. So we have pipeline, and in first approximation have that much $B \to C$ conversion going as $A \to B$. I.e. the is no "clogging" in the middle. Not much magic here.

Example 2.

Now what if we have e.g. two slow reactions as second step instead of one? Noting special: $A\to B$ , with $k1$, $B\to C$ , with $k2$, $B\to D$ , with $k3$ which translates to

$$ \frac{d[A]}{dt} = -k1 [A] $$

$$ \frac{d[B]}{dt} = k1 [A] -( k2 [B] + k3 [B])$$

$$ \frac{d[C]}{dt} = k2 [B] $$

$$ \frac{d[D]}{dt} = k3 [B] $$

Now we have the same assumption that the first step is much slower than the others than

$$ \frac{d[B]}{dt} = k1 [A] -( k2 [B] + k3 [B]) \approx 0$$

I think you can try it from here and see how the rates comes out.

Answer 3

Consider the following hourglass-analogy. The radius of mouth of each sphere indicates slowness in the sense, the slowest reaction has smallest radius.

Even though there is difference between the mouths at $B-C$ and $B-D$ junctions both are happening at same rate.This is what you thought.

But, the energy from $TS_1$has been* released in form of heat as an exotheromic reaction.Also when there is a difference in rates of r/d step this effect is diminished.

_{*Thanks to @Martin for pointing out an error}

Also, the rate of B-D and B-C are different and the products must be proportional to the rates.Otherways, the product must increase in which reaction is fast. Consider this: