Why is the enthalpy of vaporization greater than the enthalpy of fusion?

Question

Why is the molar enthalpy of vaporization of a substance larger than its molar enthalpy of fusion (at constant pressure); for example, in the case of ice and water.

Answer 1

Enthalpies of phase changes are fundamentally connected to the electrostatic potential energies between molecules. The first thing you need to know is:

There is an attractive force between all molecules at long(ish) distances, and a repelling force at short distances.

If you make a graph of potential energy vs. distance between two molecules, it will look something like this:

Here the y-axis represents electrostatic potential energy, the x-axis is radial separation (distance between the centers), and the spheres are "molecules."

Since this is a potential energy curve, you can imagine the system as if it were the surface of the earth, and gravity was the potential. In other words, the white molecule "wants" to roll down the valley until it sits next to the gray molecule. If it were any closer than just touching, it would have to climb up another very steep hill. If you try to pull them away, again you have to climb a hill (although it isn't as tall or steep). The result is that unless there is enough kinetic energy for the molecules to move apart, they tend to stick together.

Now, the potential energy function between any two types of molecules will be different, but it will always have the same basic shape. What will change is the "steepness," width, and depth of the valley (or "potential energy well"), and the slope of the infinitely long "hill" to the right of the well.

Since we are talking about relative enthalpies of fusion and vaporization for a given system, we don't have to worry about how this changes for different molecules. We just have to think about what it means to vaporize or melt something, in the context of the spatial separation or relativity of molecules, and how that relates to the shape of this surface.

First let's think about what happens when you add heat to a system of molecules (positive enthalpy change). Heat is a transfer of thermal energy between a hot substance and a cold one. It is defined by a change in temperature, which means that when you add heat to something, its temperature increases (this might be common sense, but in thermodynamics it is important to be very specific). The main thing we need to know about this is:

Temperature is a measure of the average kinetic energy of all molecules in a system

In other words, as the temperature increases, the average kinetic energy (the speed) of the molecules increases.

Let's go back to the potential energy diagram between two molecules. You know that energy is conserved, and so ignoring losses due to friction (there won't be any for molecules) the potential energy that can be gained by a particle is equal to the kinetic energy it started with. In other words, if the particle is at the bottom of the well and has no kinetic energy, it is not going anywhere:

If it literally has no kinetic energy, we are at absolute zero, and this is an ideal crystal (a solid). Real substances in the real world always have some thermal energy, so the molecules are always sort of "wiggling" around at the bottom of their potential energy wells, even in a solid material.

The question is, how much kinetic energy do you need to melt the material?

In a liquid, molecules are free to move but stay close together

This means you need enough energy to let the molecules climb up the well at least a little bit, so that they can slide around each other.

If we draw a "liquid" line approximating how much energy that would take, it might look something like this:

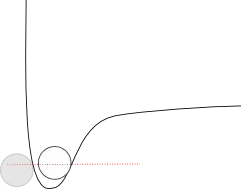
The red line shows the average kinetic energy needed for the particles to pull apart just a little - enough that they can "slide" around each other - but not so much that there is any significant space between them. The height of this line compared to the bottom of the well (times Avogadro's number) is the enthalpy of fusion.

What if we want to vaporize the substance?

In a gas, the molecules are free to move and are very far apart

As the kinetic energy increases, eventually there is enough that the molecules can actually fly apart (their radial separation can approach infinity). That line might look something like this:

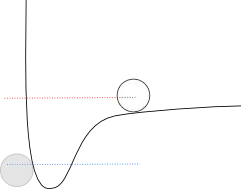
I have drawn the line a little bit shy of the "zero" point - where the average molecule would get to infinite distance - because kinetic energies follow a statistical distribution, which means that some are higher than average, some are lower, and right around this point is where enough molecules would be able to vaporize that we would call it a phase transition. Depending on the particular substance, the line might be higher or lower.

In any case, the height of this line compared to the blue line (times Avogadro's number) is the enthalpy of vaporization.

As you can see, it's a lot higher up. The reason is that for melting, the molecules just need enough energy to "slide" around each other, while for vaporization, they need enough energy to completely escape the well. This means that the enthalpy of vaporization is always going to be higher than the enthalpy of fusion.

Answer 2

The molar heat of vaporization is greater than that of molar heat of fusion due to the larger amount of energy required to break the strong attractive forces that exist between molecules of liquids than that of the attractive forces in molecules of gases.

Answer 3

Ice is less dense than water, that's why ice floats on water. The lower density of ice means that the average distance between water molecules in ice is greater than the average distance between water molecules in the liquid state. Because of the greater distance between water molecules in the solid compared to the liquid, molecule - molecule interactions (such as van der Waals and dipole interactions, as well as hydrogen bonding) will be less in the solid than the liquid. So while we need to put energy into ice to disrupt the lattice structure and break the attractive interactions, this energy is offset to some degree by the even stronger attractive forces that exist in the liquid, since the attractive forces are actually greater in the liquid than the solid.

In the gas phase the molecules are far enough apart that attractive forces between molecules are minimal. Therefor, when we go from liquid to gas we must put in a lot of energy to break all of the strong attractive forces that exist in the liquid without any offset because of the lack of significant attractive forces in the gas.

Answer 4

Enthalpy is state function which is defined as $H = U + pV$, it includes internal energy of the system and energy to create the system volume (boundary work).

Internal energy may be decomposed in several terms: oscillation around a equilibrium centre, vibrational states (stretching and bending). Generally speaking (there might be counter example for some exotic material or at temperature close to $0\ \mathrm{K}$), internal energy increase with temperature because the partition of accessible vibrational states increases (higher states activate with temperature).

About the $pV$ term, you first must consider that it cannot be negative. Therefore $H \geq U$. Now you just have to consider that, generally, $\Delta V_\mathrm{fus} < \Delta V_\mathrm{vap}$. For a given amount of matter, volume difference when melting is small before volume difference when vaporizing. This inequality holds, even for water where $\Delta V_\mathrm{fus} < 0$.

Combining those two arguments, you can explain why enthalpy of vaporization is many order of magnitude higher than enthalpy of fusion.