Simply knowing the number of teeth on a chainring can we determine an accurate diameter?
-
There are basically 3 circles with different diameters (tips of teeth, base, or where the chain actually sits) -- which one do you want? What do you need the diameter for? – freiheit Aug 04 '11 at 21:13
-
1lovely answers here, but isn't the diameter twice the radius of a circle? – jackJoe Aug 04 '11 at 21:58
-
@jackJoe yes, but that's not helpful because you don't know the radius, either. – freiheit Aug 04 '11 at 22:48
-
@JackJoe: It is. But we don't have any info besides number of teeth, per the OP. – zenbike Aug 05 '11 at 08:05
-
@freiheit & zenbike I was trying to simplify and forgot the original question, which asks for the diameter via the teeth number, so nevermind my previous comment. – jackJoe Aug 05 '11 at 09:12
-
1Dog Ears: Please do look at the question on Math.Stackexchange.com. It's a far more complex and more thorough examination of the issue. As for this page, I suggest you choose @Lantius' answer. Mine is good, and practical for most purposes. It will get within the scope of error of common measurement tools. It is not perfectly accurate, and Lantius' answer betters that. – zenbike Aug 05 '11 at 15:54
3 Answers
A chainring is an n-sided regular polygon where n is the number of teeth. The side length s of the polygon is the distance from tip-to-tip of each chainring tooth.
The formula for radius of a regular polygon is:

(source: mathopenref.com)
Using zenbike's 12.75mm above for s, we get 107.61 for the radius, or 215.22mm for the diameter, which is very close to his approximation.
Comparing the two formulas shows that the length term, as expected, can be eliminated. This leaves us with:
1 / sin( pi / n ) vs. n / pi
For large n, those terms converge, introducing an error of just .12mm when n=53. It's a bit larger as n gets smaller, differing by .64mm for n=11.
For all practical purposes, I'd just use s * n / pi, even for the smallest cog you'll come across it'll be within a millimeter.
-
I'm interested in the math here. Can you spell out (for those of us with less time in a math class) what each variable represents? I think I'm following you, but I'm not certain. The s*n/pi formula is the same as what I'm doing, correct? Where does the inaccuracy for a smaller number of sides come from? (Assuming I'm following you and have the variables right. ) – zenbike Aug 05 '11 at 08:14
-
-
1It's a straight line. For example, if you had an impossibly-tiny chainring with eight teeth (vertices), you could trace a clean-looking octagon around it. As you have surmised, measuring the straight-line distance along the edges of that octagon and multiplying is missing the extra bit of distance that an arc would scribe between those points, so your total circumference comes out just a bit short. As your points get closer together, the difference gets smaller - a polygon with a million tiny sides is going to be nearly indistinguishable from a circle. – lantius Aug 05 '11 at 09:08
-
That's what figured. Thanks for the clarification. So how do you adapt for the missing arc in the measurement? – zenbike Aug 05 '11 at 09:12
-
As far as the math: You construct a right triangle with three points: the middle of a side, an adjacent vertex, and the center of the polygon - as in this image. The hypotenuse will be the radius you are looking for. The opposite side will be of length (s/2). Since (2n) of these triangles would make a complete revolution (2pi radians), the angle in the middle is (pi/n) radians. From trigonometry (SOH CAH TOA), therefore: sin(pi/n) = (s/2) / r. Move the terms about with algebra and you get the formula above. – lantius Aug 05 '11 at 09:24
-
Thanks. I'll try to work through that. I may bug you again if i get stuck. – zenbike Aug 05 '11 at 09:33
-
1The same mathematics in a slightly easier to digest format is the crd(theta) function http://en.wikipedia.org/wiki/Chord_(geometry) - it relates the length of the chord (the chain pitch in this case) to the radius and the angle. Adapted here, 12.7mm = r crd (360 / n) = 2rsin(180 / n); therefore r = 6.35 / sin (180 / n) mm. We need TeX over here. – Ehryk Jun 03 '12 at 03:46
If you only know the pitch of the chain (standard for most bicycles) and number of teeth, then you can fully describe the circle (and n-gon) through the pin centers only. I will do my best to do the math formulas in a readable way with text, but I will fully describe each of the four circles/n-gons:

Let:
n = number of teeth
L = chain pitch (link length) (12.7mm for most bicycles)
See below for valley, roller top, and tooth top measurements. Note that tooth tops can vary between manufacturers and will vary throughout the life of the ring. The alternate method at the bottom is probably the easiest method to use for frame clearance.
Since you know the pitch of the chain (1/2" or 12.7mm is a 40 series chain typically used on a bicycle), the chain-pins will form a regular n-gon (a polygon with n-sides of equal length), with each side being equal to 12.7mm. The formula for the perimeter of this n-gon is rather simple (below) and would be fine for most approximations. Note that this is also equal to the chain length that would be wrapped around the ring (the chain would follow the n-gon, not the circle).
Perimeter of n-gon made by pin centers
Perimeter of n-gon = L * n = 12.7 * n mm
However, this is not entirely accurate to describe the circle through the pin centers. The more accurate formulas are below:
Circle through pin centers
circumference = pi * L / (sin (180 / n)) = 39.8982 / (sin (180 / n)) mm
radius = L / (2 sin (180 / n)) = 6.35 / sin (180 / n) mm = 'pcRad' (pin center radius)
diameter = L / sin (180 / n) = 12.7 / sin (180 / n) mm = 'pcD' (pin center diameter)
Now, we will need additional information to describe the two related circles / n-gons:
For the valley floors and roller tops, we need to know the radius or diameter of the chain roller around the pin. According to http://en.wikipedia.org/wiki/Roller_chain, a 40 series chain has a roller-diameter of 0.312" (7.92mm). Since the distance from pin-center to the bottom of the valley is the radius of the roller:
Circle / n-gon about valley floors
rRad = roller radius (3.96 mm for most bicycles)
Perimeter of n-gon of valley floors = 2 * n * (pcRad - rRad) * sin (180 / n)
= 2n * (pcRad - 3.96) * sin (180 / n) mm
floorRadius = pcRad - rRad = pcRad - 3.96 mm
floorDiameter = 2 * fRad = pcD - 2 * rRad = pcD - 7.92 mm
Circle / n-gon of the tops of the chain rollers
Perimeter of n-gon of roller tops = 2 * n * (pcRad + rRad) * sin (180 / n)
= 2n * (pcRad + 3.96) * sin (180 / n) mm
rollerTopRadius = pcRad + rRad = pcRad + 3.96 mm
rollerTopDiameter = 2 * rtRad = pcD + 2 * rRad = pcD + 7.92 mm
rollerTopCircumference = pi * rtD = pi * (pcD + 2 * rRad) = pi * (pcD + 7.92) mm
Now, for the final circle / n-gon to describe, we need the tooth height above the pin centers. I would expect this to be positive on a new chain ring and negative on a worn one:
Circle / n-gon of the tooth tips
t = tooth tip height above pin centers (negative if below)
Perimeter of n-gon of tooth tips = 2 * n * (pcRad + t) * sin (180 / n)
tipRadius = pcRad + t
tipDiameter = 2 * tRad = pcD + 2 * t
tipCircumference = pi * tD = pi * (pcD + 2 * t)
Alternatively, to make this computation a bit easier (yet slightly less accurate on a worn chain ring), you can measure your own individual tooth spacing. Ideally they would be slightly longer than the chain pitch, but that will change as the chain wears:
Circle / n-gon of the tooth tips - Alternate
tSpacing = average distance between tooth tips
Perimeter of n-gon of tooth tips = n * tSpacing
tipRadius = tSpacing / (2 sin (180 / n))
tipDiameter = 2 * tRad = tSpacing / sin (180 / n)
tipCircumference = pi * tD = pi * tSpacing / (sin (180 / n))
-
A small correction to Ehryk's formulas related to valley floors and tips. According to [1], a 40 series chain has roller diameter of 7.77mm (0.306 inches). Ehryk's is for a 41 series chain. [1]: http://en.wikipedia.org/wiki/Roller_chain – Apr 03 '15 at 17:25
EDIT:
I posted this question on math.se, and got an interesting answer, which basically confirms Lantius' answer as the more accurate mathematical model, and mine as a practical approximation for the bicycle world.
With only the number of teeth, no.
But given the number of teeth, and the required spacing from tip to tip of each tooth to match the chain for the brand of chain ring used, you can easily determine the circumference.
With the circumference, it's simple math to determine the diameter.
Divide the diameter by Pi (3.14159 to the 5th decimal)
C = D/3.14159
So if the number of teeth is 53, and the spacing is 12.75mm, we have a circumference of 675.75 millimeters.
675.75 millimeters divided by 3.14159 gives a diameter of 215.1 millimeters. Converted and rounded to 2 places, it's 8.46 inches.
I've measured the diameter of a 53 tooth Shimano chain ring, and it is 8.51 inches. So I believe my math should be as accurate as the tolerances in my measurements.
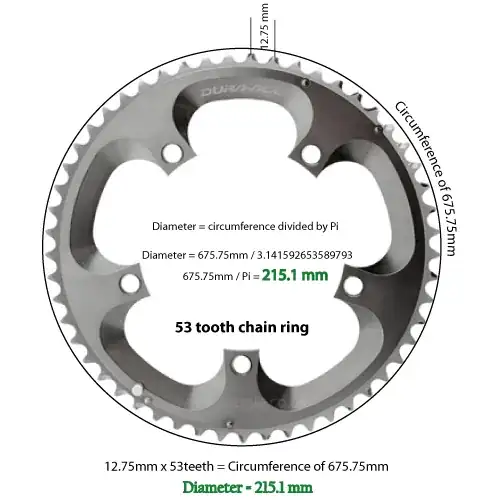
-
Of course, with a chainring you have the question of what is "the diameter" -- how do you measure it? When calculated from the above formula you should get the diameter of the chain circle -- basically the circle that the chain pins describe -- not the innermost or outermost diameter. – Daniel R Hicks Aug 04 '11 at 11:17
-
Actually, this number is based on the measurement with a vernier caliper from tip of tooth to tip of tooth. It is the circumference described by a circle placed to touch the tip of each tooth. And I did assume outside diameter, since that is what would matter for framebuilding. – zenbike Aug 04 '11 at 11:59
-
3
-
Yeah, now that I think about it a chain should be slightly loose on a chainring -- one way to (crudely) check for chain stretch is to pull out on the front-most link and see how much it gives -- should be about half a chain thickness. But still you wouldn't (in theory, at least) be calculating the outermost diameter with your formula. – Daniel R Hicks Aug 04 '11 at 12:19
-
@Daniel R Hicks: How is that? It does in fact work, as I did the math, and checked it against a physical chain ring, and it matches. Am I not describing the process well enough, maybe? – zenbike Aug 04 '11 at 12:42
-
according to http://en.wikipedia.org/wiki/Bicycle_chain all chains have a pitch of 1/2" (ANSI Standard #40) – Dog Ears Aug 04 '11 at 13:10
-
The pitch circle diameter is different from the tooth circle diameter. Which do you want? You can use one 1/2 inch in the above formula for pitch circle diameter. For tooth circle diameter, you need a measurement, or average measurement from the center of tip to the center of tip. If you want pitch base circle diameter, you need a center of valley to center of valley measurement. With appropriate input, the above formula will provide all of the above. And note, it says modern bicycle. Not all bicycles. – zenbike Aug 04 '11 at 13:33
-
-
@zenbike -- I don't offhand know why you came so close to the outermost diameter using that formula. I would have expected you to be shy by 1/2 inch or so. One of life's mysteries, I suppose. – Daniel R Hicks Aug 04 '11 at 17:32
-
@Daniel R Hicks: I really don't understand why you get that impression. If I measure the distance from the center of the top of each tooth, to the next tooth, and multiply by the number of teeth, that has to give me the circumference. If I divide the circumference by Pi, I get the Diameter. If I'm wrong, I'm wrong, but I'm not. i've tested it on 6 different chainring sizes and brands at this point, and I'm within 1.5 mm of the physically measured diameter on each of them. That's as accurate as I can expect with the tools I have to measure. If you think different, give me a corrected formula. – zenbike Aug 04 '11 at 17:47
-
By the way, diameter is the distance across the center of a circle not the distance around it. Outermost diameter doesn't make sense. – zenbike Aug 04 '11 at 17:49
-
But the center of tooth tip to tooth tip should not be 1/2 inch, but something a hair greater. As the chain peels off the sprocket, the last link touching the sprocket with both pins touches the tip of one tooth and a bit farther down on the next. Similarly, the next link touches the third tooth even farther down. The profile of the teeth is such that this relationship is maintained for each link and tooth until the chain reaches the tangent point with the sprocket. – Daniel R Hicks Aug 04 '11 at 19:29
-
And, by the way, if you measure tooth-top to tooth-top and multiply by the number of teeth you'll get something (slightly) less than the circumference of the containing circle. – Daniel R Hicks Aug 04 '11 at 19:32
-
Again, since I've done the math, and the physical measurements, and they match, you'll have to do more than just say that to convince me. Where is your formula or answer? And what exactly is it that you think I've done wrong? For the record, the measurement I used in my calculation was 12.75mm, tooth tip to tooth tip. – zenbike Aug 04 '11 at 19:41
-
@Daniel R Hicks, I've added a diagram, to hopefully eliminate whatever confusion of communication we're having. The math is right, though, unless you can point out a specific error? – zenbike Aug 04 '11 at 20:35
-
@Daniel R Hicks: FWIW, 12.75mm is .502 inches. So slightly more than 1/2 inch, but not enough for the 1/2 inch difference you're saying I should see/expect. – zenbike Aug 04 '11 at 20:46
-
@DanielRHicks is correct; but this should still fall within your 1.5mm margin. The reason is that you're making the n-gon discussed above, so the circumference != center of top tooth to next tooth * number of teeth; this is the perimeter of the n-gon at the tooth-tops. I too was surprised how little of a difference this makes (like Dan I was expecting it to be off more) but the proper formula for the circumference through the pin centers = pi * (link length) / sin (180 / n). Using this, I get d = 215.223mm and c = 676.146mm – Ehryk Jun 03 '12 at 01:12
-
We were looking for tooth circle diameter, not pin center. The point was to judge the clearance to the frame with a chainring which is not in hand. if, say, I have a 42t chainring in place, and want to know how much larger a 46t would be, before I buy it. I understand what you're saying, and Lantius is right, which is why I suggested his answer be accepted. @DanielRHicks was wrong, if only because his measurements don't match the physical ones, and he wouldn't explain what his process was, or why he thought mine was wrong. – zenbike Jun 03 '12 at 02:26
-
See my answer below. Tooth tip height cannot be calculated this way (without knowing the distance of the tooth tips from pin centers); so if that's the point of the question, the answer is no in a definitive sense (though it'd surely be in the ball park, as you measured experimentally). Note that neither of the reasons you gave make @DanielRHicks wrong. I hope my answer illustrates why he is correct, although your experimental results are 'close enough' for the purpose of the question. – Ehryk Jun 03 '12 at 02:51
-
@Ehryk, Daniel was wrong because his expected result was 1/2" off of measured reality, and he wouldn't or couldn't give any explanation why. This has been discussed to death, and you answer duplicates the accepted answer. Why are we talking about it again? – zenbike Jun 03 '12 at 04:57
-
His expected result was off, and I mentioned I was also surprised by how little, however he was correct that the formula would be 'shy some.' He also is not wrong BECAUSE he didn't give explanation, and you aren't correct until proven wrong. Correctness has nothing to do with explanation or lack thereof. "The math is right, though, unless you can point out a specific error?" is shifting the burden of proof - the math is either correct or incorrect, and nL = the perimeter of the 53-gon, not the circumference of the circle you drew (piL/sin(180/n)). – Ehryk Jun 03 '12 at 05:41
-
I didn't say I was right. I said @Lantius was correct. I just said Daniel wasn't right. The quote you are using above is out of context. I wasn't creating a proof. My proof was that the measurement matched the formula's result. Asking for Daniel to tell me where I was wrong, if he thinks I was, was not "shifting the burden of proof". It was asking him to detail his proof of the assertion he made that I was wrong. Either way, this whole convo is long done, and I'm not going to rehash it with you, a person who was in no way involved. Have a nice day. – zenbike Jun 03 '12 at 07:20
-
I said Of course, with a chainring you have the question of what is "the diameter" -- how do you measure it? When calculated from the above formula you should get the diameter of the chain circle -- basically the circle that the chain pins describe -- not the innermost or outermost diameter. I did make the slight faux pas in that I should have said "N-gon" rather than circle, but the main point is that the calculation must be through the pin centers, not the tooth tips. If don't see how this should even require explanation. – Daniel R Hicks Jun 03 '12 at 10:58
-
You can calculate the tooth tip diameter once you relax the idea of using the chain pitch - which @zenbike is not. The chain pitch is 12.7mm (ideally), but he's using the tooth-tooth measurement which he has at 12.75mm. n * this measurement = the perimeter of the 53-gon about the teeth = 675.75mm, but the circumference will be slightly greater (pi*12.75/sin(180/53)) = 676.14mm. The caveat here is that you need to measure each tooth-spacing because they will vary from chainring to chainring, where the pitch will not. – Ehryk Jun 03 '12 at 11:29
-
@DanielRHicks: It doesn't require explanation. We worked through this long ago. It was settled, long ago. Ehryk is just trying to stir things up, as is his habit. And he's annoyed that I've told him I'm not interested in hearing from him about it. Lastly, I know you were saying that a half inch pitch multiplied that way would give you pitch circle, not diameter, but I was using the tip to tip measurement, not set pitch, and as I've said before, that has to give you the tooth tip diameter, at least within a close margin of error. – zenbike Jun 03 '12 at 11:57
-
I am not interested in 'stirring things up' and if you think that is my motivation then you have me completely misunderstood. I have pointed out errors and misunderstandings (not just in the comment you deleted), and you are committing logical fallicies when you say things like "X is wrong because they didn't explain it to me or didn't debunk my theory/equation". Then you deny that you're shifting burden of proof when this is a textbook case thereof. Further, I am somewhat dismayed at the lack of even attempting to understand, or consider you could be in error - you just cut off discussion. – Ehryk Jun 03 '12 at 13:23
-
This is not a discussion forum. It's a Q&A site. I tried politely telling you this has all been hashed out months ago, and you refuse to hear it. I don't particularly care whether you are happy about it, or think that my thoughts or methods aren't valid. You refuse to recognize the fact that you are late to the party, and that you are bringing nothing new to the discussion. Neither you nor Daniel have been willing or able to answer the only unanswered question here: If, as you state, I am wrong, why do the measurements work out as I predict? – zenbike Jun 03 '12 at 14:11
-
Lantius, when he presented the possibility that I was wrong, had both a reason, and a better answer. And what was my response? I researched it. I asked him to explain it. Then I agreed with him, and suggested that the OP choose his answer. My answer is close enough for the approximation. His was correct. There is nothing left to discuss. And I'm done with this conversation. – zenbike Jun 03 '12 at 14:14
-
Also, I didn't delete your comment. I flagged it for rudeness. I didn't delete any of the other places where the same statements were made, because they were done reasonably politely. – zenbike Jun 03 '12 at 14:16
-
Why would time be of any consequence here? Wrong is wrong, and has no temporal limit where it becomes not wrong. Further, I didn't see these answers clearly enough showing how to describe ALL a chainring's measurements, and the question does not specify tooth-tip diameter. Your measurements work out because your formula is 'good enough' for the margin of error you care about. What my comment was intended to elucidate is that Daniel's comments were all correct except the "1/2" or so", but more importantly the REASONING by which you were claiming him wrong is invalid, and I described why. – Ehryk Jun 03 '12 at 21:55
-
@zenbike - I would very much appreciate it if you would discuss this with me in chat. – Ehryk Jun 03 '12 at 22:32