Would a Sears–Haack body have the same wave drag as the same body with cylinder of the same diameter placed in the middle, between two halves of the Sears–Haack?
Asked
Active
Viewed 1,321 times
2 Answers
3
No it will not have the same wave drag.
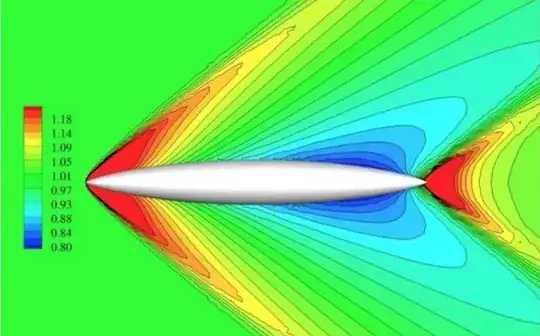
The low wave-drag of a Sears-Haack-Body is achieved by the smoothness of the body. This means kinks are not allowed. The picture below shows the Mach-Number distribution around a Sears-Haack-Body (taken from YAMAZAKI 2014). Notice the gradual change of the Mach number along the body surface .
The following illustration shows the proposed elongation of the body by inserting a cylinder.
By adding a cylinder the curvature of the body does not change gradually (smoothly) but stops - stays constant - and starts again.
This will trigger a Prandtl-Meyer-expansion (example below, taken from here) which will distort the smooth flow around the body and thereby increase the wavedrag.
rul30
- 1,547
- 12
- 24
0
Wave drag of a body of revolution depends on volume, so increasing the volume of an already minimum wave drag body will increase its wave drag. When you lengthen the center section you increase the volume of the body and therefore the drag, and since the resulting shape is not Sears-Haack the drag is even higher.
See Computing Supersonic Volume Wave Drag halfway down the page.
Pilothead
- 20,096
- 3
- 54
- 98
-
Actually, according to the link drag is proportional to v^2/l^4. Since im only making the body longer volume and length change by the same ratio, and as the length is raised to higher power the drag will actually decrease, correct? – Francis L. May 22 '18 at 01:29
-
1@FrancisL. Look farther down the page. What it means is that wave drag depends on volume, and a Sears-Haack body gives the lowest drag for a given volume. When you lengthen the center section you increase the volume of the body and therefore the drag, and since the resulting shape is not Sears-Haack the drag is even higher. – Pilothead May 22 '18 at 02:03