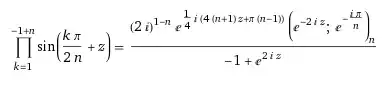A well know trigonometric identity states that for all $z$: $$\prod_{k=1}^{n-1}\sin\left(\frac{\pi k}{n}+z\right)=\frac{2}{2^{n}}\csc\left(z\right)\sin\left(nz\right)$$
Is there any such formula for the quantity: $$P(n,z)=\prod_{k=1}^{n-1}\sin\left(\frac{\pi k}{2n}+z\right)$$
I'm particularly interested in lower and upper bounding the ratio $$\frac{P^2(n,\alpha/n)}{P^2(n,\beta/n)}$$ when $n$ grows large.